Solving word problems is one of the most common reasons to use a system of equations. For example, some word problems in the ACT Math test that would be difficult to approach using a single variable are relatively easy when you use more than one variable.
A system of equations is a set of two or more equations that include two or more variables. To solve a system of equations, you need one equation for every variable in the system. This usually means two equations and two variables.
Example
Dorian and Micah have been saving money from their summer jobs. If Dorian had twice as much money and Micah had half as much, together they would have $2,075. And if Micah had twice as much money and Dorian had half as much, together they would have $2,300. How much money does Dorian have?
(A) $800
(B) $850
(C) $900
(D) $950
(E) $1,000
You could solve this problem using only one variable, but that approach would be tricky and would likely lead to a mistake along the way. Instead, use two variables, letting d equal Dorian’s money and m equal Micah’s money. Set up two equations as follows:
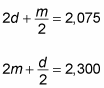
To eliminate the fractions, multiply both of these equations by 2:
This system of equations is easy to solve using substitution. Begin by isolating m in the first equation:
m = 4,150 – 4d
Now substitute 4,150 – 4d for m in the second equation, and then solve for d:
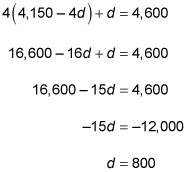
Dorian has $800, so the correct answer is Choice (A).





