Here are a few things you need to know about angles to succeed on the ACT:
- Angles that are greater than 0 but less than 90 degrees are called acute angles. Think of an acute angle as being a cute little angle.
- Angles that are equal to 90 degrees are called right angles. They’re formed by perpendicular lines and indicated by a box in the corner of the two intersecting lines.
Don’t automatically assume that angles that look like right angles are right angles. Without calculating the degree of the angle, you can’t know for certain that an angle is a right angle unless one of the following is true:
-
- The problem directly tells you, “This is a right angle.”
- You see the perpendicular symbol, indicating that the lines form a 90-degree angle.
- You see a box in the angle, like the one in the following figure.
- Angles that are greater than 90 degrees but less than 180 degrees are called obtuse angles. Think of obtuse as obese; an obese (or fat) angle is an obtuse angle.
- Angles that measure exactly 180 degrees are called straight angles.
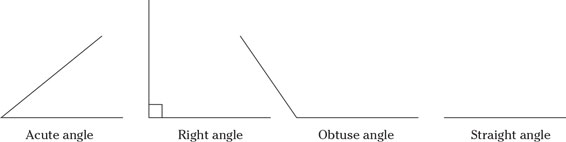 Basic angles.
Basic angles.- Angles that total 90 degrees are called complementary angles. Think of C for corner (the lines form a 90-degree corner angle) and C for complementary.
- Angles that total 180 degrees are called supplementary angles. Think of S for supplementary (or straight) angles. Be careful not to confuse complementary angles with supplementary angles. If you’re likely to get them confused, just think alphabetically: C comes before S in the alphabet; 90 comes before 180 when you count.
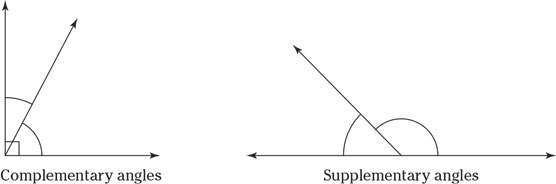 Complementary and supplementary angles.
Complementary and supplementary angles.- Angles that are greater than 180 degrees but less than 360 degrees are called reflex angles.
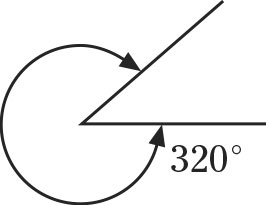 Reflex angle.
Reflex angle.- Angles around a point total 360 degrees.
- The exterior angles of any figure are supplementary to the two opposite interior angles and always total 360 degrees.
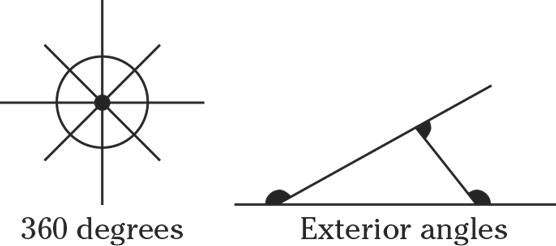 Angles that measure 360 degrees.
Angles that measure 360 degrees.- Angles that are opposite each other have equal measures and are called vertical angles. Just remember that vertical angles are across from each other, whether they’re up and down (vertical) or side by side (horizontal). (The following figure shows two sets of vertical angles.)
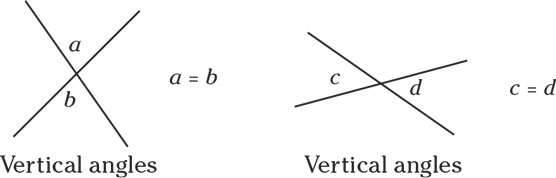 Vertical angles have equal measures.
Vertical angles have equal measures.- Angles in the same position around two parallel lines and a transversal are called corresponding angles and have equal measures. (The following figure shows two sets of corresponding angles.)
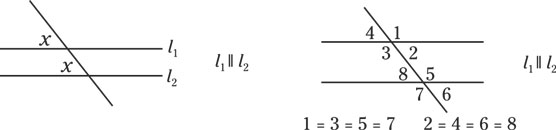 Corresponding angles have equal measures.
Corresponding angles have equal measures.When you see two parallel lines and a transversal (that’s the line going across the parallel lines), number the angles. Start in the upper-right corner with 1 and go clockwise. For the second batch of angles, start in the upper-right corner with 5 and go clockwise. Note that in the preceding figure, all odd-numbered angles are equal and all even-numbered angles are equal.
Be careful not to zigzag back and forth when numbering. If you zig when you should have zagged, you can no longer use the tip that all even-numbered angles are equal to one another and all odd-numbered angles are equal to one another.




