Statistical Analysis with Excel For Dummies
Book image
Explore Book Buy On Amazon
Huh? Is that correct? Two-Factor??? Without Replication?? Is this real, Excel? What’s that all about? Here's the story: If you’re looking through the data analysis tools for something like Anova: Single Factor Repeated Measures, you won’t find it. The tool you’re looking for is there, but it’s hiding out under a different name.

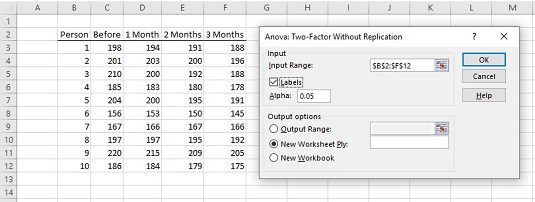
Anova: Two Factor Without Replication data analysis tool
 The Anova: Two Factor Without Replication data analysis tool dialog box.

The steps for using this tool are:

  1. Type the data for each sample into a separate data array. Put the label for each person in a data array. For this example, the labels for Person are in column B. The data in the Before sample are in column C, the data in the 1 Month sample are in column D, the data for the 2 Month sample are in column E, and the data for the 3 Month sample are in column F.
  2. Select DATA | Data Analysis to open the Data Analysis dialog box.
  3. In the Data Analysis dialog box, scroll down the Analysis Tools list and select Anova: Two Factor Without Replication.
  4. Click OK to open the select Anova: Two Factor Without Replication dialog box.
  5. In the Input Range box, type the cell range that holds all the data. For the example, the data are in $B$2:$F$12. Note the $ signs for absolute referencing. Note also — and this is important — the Person column is part of the data.
  6. If the cell ranges include column headings, select the Labels option. The headings were included in the ranges, so the box was selected.
  7. The Alpha box has 0.05 as a default. Change the value if necessary.
  8. In the Output Options, select a radio button to indicate where you want the results. New Worksheet Ply was selected so Excel would put the results on a new page in the worksheet.
  9. Click OK. A newly created page opens with the results because New Worksheet Ply was selected.
The output features two tables: SUMMARY and ANOVA.

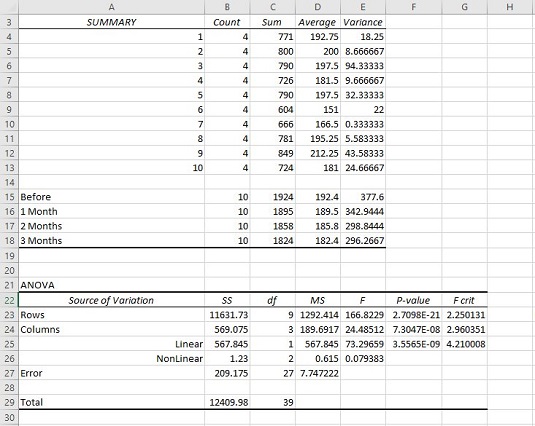
Excel output
 Output from the Anova: Two Factor Without Replication data analysis tool.

The SUMMARY table is in two parts. The first part provides summary statistics for the rows. The second part provides summary statistics for the columns. Summary statistics include the number of scores in each row and in each column along with the sums, means, and variances.

The ANOVA table presents the Sums of Squares, df, Mean Squares, F, P-values, and critical F-ratios for the indicated df. The table features two values for F. One F is for the rows, and the other is for the columns. The P-value is the proportion of area that the F cuts off in the upper tail of the F-distribution. If this value is less than .05, reject H0.

Although the ANOVA table includes an F for the rows, this doesn’t concern you in this case, because H0 is only about the columns in the data. Each row represents the data for one person. A high F just implies that people are different from one another, and that’s not news.

About This Article

This article is from the book:

About the book author:

Joseph Schmuller works on the Digital & Enterprise Architecture Team at Availity. He has taught statistics at the undergraduate and graduate levels. He has created and delivered courses for LinkedIn Learning, and he is the author of all previous editions of Statistical Analysis with Excel For Dummies.

This article can be found in the category: