Consider the We Are Jeans store. It costs the business $29 to make a pair of jeans. This includes materials and labor. There’s also the fixed cost amount to consider. Fixed costs can include salaries of employees, insurance, mortgage payments, equipment, and so on. The fixed costs are shared by all the different products sold. In this case, for the jeans, the fixed costs come to $1,000. The store sells the jeans for $49 per pair. How many pairs of jeans do they have to sell to start making a profit on them? What is the break-even point?
First, write equations to model the situation. For the cost function, you have C(x) = 29x + 1,000, where x is the number of pairs of jeans. And the revenue function is R(x) = 49x.
To put this in terms of equations in a coordinate plane, just write the functions as y = 29x + 1,000 and y = 49x. The figure shows what these functions look like when you graph them.
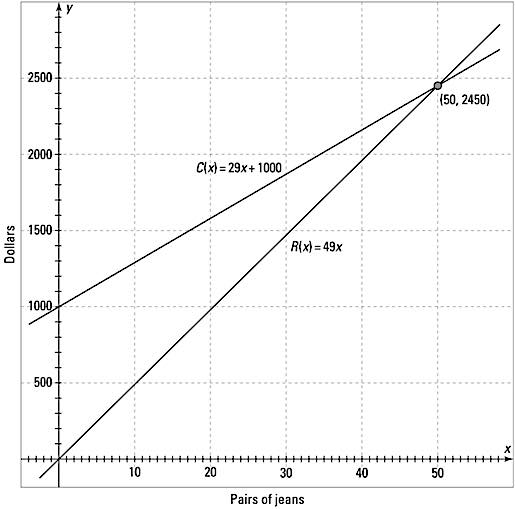 Cost and revenue functions intersect at the break-even point.
Cost and revenue functions intersect at the break-even point.To find the solution of the system of equations y = 29x + 1,000 and y = 49x, the simplest thing to do is to use substitution, because they’re both already solved for y. Setting the two y’s equal to one another, you get 29x + 1,000 = 49x. Subtracting 29x from each side, you then get 1,000 = 20x. Dividing each side by 20, you have that x = 50.
Because x is the number of pairs of jeans, it takes the sale of 50 pairs of jeans to break even. The cost to produce 50 pairs of jeans is $2,450, and the revenue from 50 pairs of jeans is $2,450. Selling more than 50 pairs of jeans results in a profit.





