An argument can be classified as either valid or invalid. A valid argument occurs in situations where if the premises are true, then the conclusion must also be true. And an argument can be valid even if the conclusion is false.
The following argument has two premises: (1) “All dogs have fleas.” (2) “Hank is a dog.” The conclusion is that, therefore, Hank has fleas.These arguments usually have the following format with the premises listed first and the conclusion under a horizontal line:
Using an Euler diagram to analyze this argument, draw a circle to contain all objects that have fleas. Inside the circle, put another circle to contain all dogs. And inside the circle of dogs, put Hank. The figure illustrates this approach.
Poor Hank has fleas.The argument isn’t necessarily true, because you know that not all dogs have fleas. All this shows is that the argument is valid. If the two premises are true, then the conclusion must be true.
Now consider an argument involving rectangles and triangles. A polygon is a figure made up of line segments connected at their endpoints.
When analyzing the validity of this argument, the Euler diagram starts with a circle containing all polygons, as shown here.
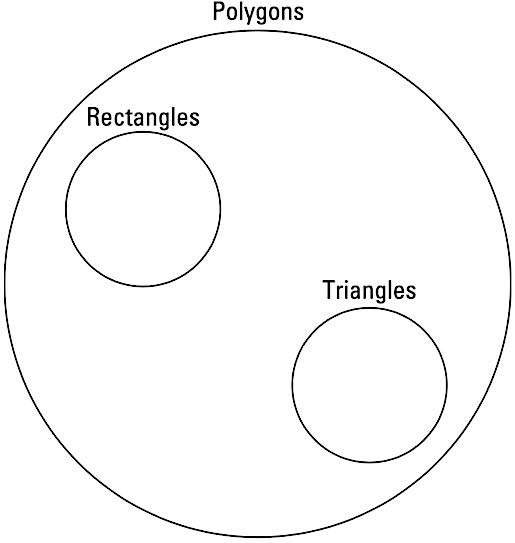Two types of polygons.Two circles are drawn inside the larger circle—one containing rectangles and the other triangles. The two circles don’t overlap, because rectangles have four sides, and triangles have three sides.
The argument is invalid. Rectangles are not triangles—not even sometimes.
Arguments can have more than two premises. For example:
One Euler diagram that can represent this situation has three intersecting circles, as shown here.
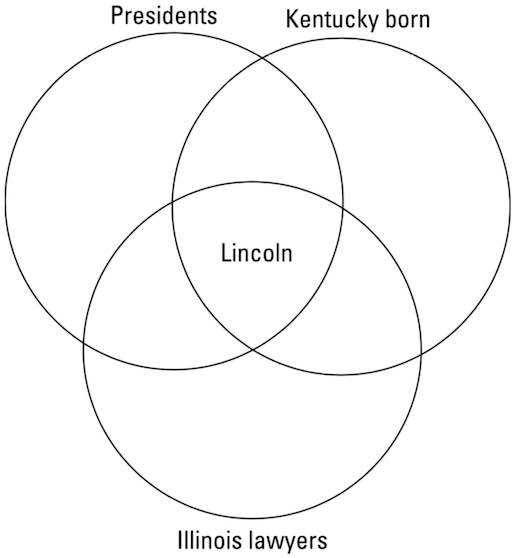President Abraham Lincoln and other Illinois lawyers.As you can see from the diagram, there can be presidents born in Kentucky who were not lawyers in Illinois and there can be presidents who were lawyers in Illinois but not born in Kentucky. The argument is invalid. To be valid, it must always be true.