In the binomial formula, you use the combinations formula to count the number of combinations that can be created when choosing x objects from a set of n objects:
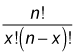
One distinguishing feature of a combination is that the order of objects is irrelevant.
For example, you can use this formula to count the number of ways you choose two elective classes from a set of eight for the upcoming semester. The order in which you choose the electives is immaterial; each possible selection is a combination of two objects.
As another example, suppose that you're painting your house with two colors from a set of four: green, blue, white, and yellow. Because the order in which you choose the colors is irrelevant, each pair of colors is a combination. How many different color schemes are possible with the given set of choices? You can answer this question by simply listing all the possible combinations:
green, white
green, blue
green, yellow
white, yellow
white, blue
blue, yellow
This list shows that you have six possible choices of pairs of colors.
The quicker way to answer this question is to substitute these values into the combinations formula; in this case, x represents the number of colors to choose (2), and n represents the total number of colors you can choose from (4).
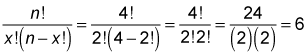
The formula for computing the number of combinations is sometimes expressed as
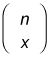
Read or say this expression as "n choose x." This function appears on many calculators as nCr. In Microsoft Excel, you can compute combinations with the function COMBIN.
When you're selecting x objects from a group of n objects in such a way that the order of selection does matter, the choices are known as permutations instead of combinations.





