If you have trouble solving an ACT math question, you can apply different strategies with the given answer choices to help you determine which choice is correct. The math section of the ACT is comprised of 60 multiple-choice questions. Each question provides five possible answers. Every multiple-choice question gives you a little extra information, because you know the correct answer must be one of the five choices given. Always take a moment to notice these answer choices, because they may guide you as you work on solving the problem.
The following example shows you how you can rely on answer choices to correctly solve a problem.
Example 1
If j2 – 14j + 48 = 0, which of the following shows all of the possible values of j?
(A) –6
(B) 8
(C) 6, 8
(D) –6, 8
(E) –6, –8
You can solve the equation j2 – 14j + 48 = 0 by factoring. In this case, every value in each of the five answers includes either 6 or 8 (give or take a minus sign), so you have a head start on the factoring:
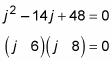
At this point, you only need to fill in the signs (+ or –) inside the parentheses. Because 48 in the original equation is positive, the two signs must be the same (either both + or both –). And because –14 is negative, at least one of the signs is negative. Therefore, both signs are negative:
Now you can solve this equation by breaking it into two separate equations:
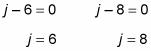
Thus, the correct answer is Choice (C).
Multiple-choice questions also give you an opportunity to arrive at the correct answer by plugging in the answer choices and solving. Note that plugging in answers can be a little time-consuming, so if you can find a better way to solve the problem, go for it. But when you get stuck, this tactic gives you a chance at answering questions that you really aren’t sure how to solve. Consider the following example.
(A) 4
(B) 5
(C) 6
(D) 7
(E) 8
You may or may not know how to solve this type of equation. And in any case, solving it may be time-consuming. So you can try to plug in each possible answer for x to see which one works. Start with Choice (A) and plug in 4 for x:
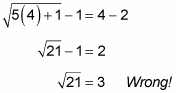
This answer choice is obviously wrong, because 21 isn’t a square number. Therefore,
is irrational and doesn’t equal 3. In fact, this wrong answer choice may suggest a way to save even more time: The reason this answer is wrong is that the value of
evaluates to an irrational number, which messes up the equation. So
has to be a rational number, which means 5x + 1 must be a square number. Try testing Choices (B) through (E) in this way, keeping in mind that you’re looking for a value of x that makes 5x + 1 a square number:

Only one value produces a square number, so the correct answer is Choice (D). You can verify this by plugging in 7 for x:
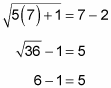
Some questions ask you for the greatest or least number that has a certain property. These questions provide a great opportunity to test answers individually until you find the correct one. Consider the following strategies:
When looking for the lowest or least value, begin with the lowest number and work your way up.
When looking for the greatest or highest value, begin with the greatest number and work your way down.
The following example illustrates this strategy.
Example 2
What is the least common denominator when adding three fractions with denominators of 6, 9, and 16?
(F) 60
(G) 120
(H) 144
(J) 240
(K) 288
Because you’re looking for the least common denominator, you can find the correct answer by testing numbers and ruling out wrong answers, starting with the lowest number.
Begin by testing to see whether 60 is divisible by 6, 9, and 16:
So Choice (F) is wrong. Now test 120:
So Choice (G) also is wrong. Next, test 144:
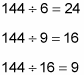
So Choice (H) is the correct answer. By the way, notice that 288 is also divisible by all three denominators. However, Choice (K) is wrong because the question asks for the least common denominator, which is why you started plugging in the lowest numbers first.





