The RL time constant indicates the amount of time that it takes to conduct 63.2% of the current that results from a voltage applied across an inductor. The value 63.2% derives from the calculus equations used to determine the exact time constants for both resistor-capacitor and resistor-inductor networks.
Here's the formula for calculating an RL time constant:
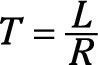
In other words, the RL time constant in seconds is equal to the inductance in henrys divided by the resistance of the circuit in ohms.
Suppose the resistance is 100 Ω, and the capacitance is 100 mH. Before you do the multiplication, you first convert the 100 mH to henrys. Because one millihenry (mH) is one, one-thousandth of a henry, you can convert millihenrys to farads by dividing the millihenrys by 1,000. Therefore, 100 mH is equivalent to 0.1 H. Dividing 100Ω by 0.1 F gives you a time constant of 0.001 second (s), or one millisecond (ms).
The following gives you a helpful approximation of the percentage of current that an inductor passes after the first five time constants. For all practical purposes, you can consider the current fully flowing after five time constants have elapsed.
| RL Time Constant Interval | Percentage of Total Current Passed |
|---|---|
| 1 | 62.3% |
| 2 | 86.5% |
| 3 | 95.0% |
| 4 | 98.2% |
| 5 | 99.3% |
Thus, in a circuit in which the resistance is 100 Ω and the inductance is 0.1 H, you can expect that current will be flowing at full capacity within 5 ms of when the voltage is applied.
Five milliseconds is a very short amount of time. But electronic circuits are often designed to respond within very short time intervals. For example, the sine wave of standard household alternating current swings from its peak positive voltage to its peak negative voltage in about 8 ms.
Sound waves at the upper end of the human ear's ability to hear cycle in about 25 μs (microseconds), and the time interval for radio waves can be in small fractions of microseconds. Thus, very small RL time constants can be very useful in certain types of electronic circuits.





