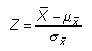In statistics, sampling distributions are the probability distributions of any given statistic based on a random sample, and are important because they provide a major simplification on the route to statistical inference. More specifically, they allow analytical considerations to be based on the sampling distribution of a statistic, rather than on the joint probability distribution of all the individual sample values.
The value of a sample statistic such as the sample mean (X) is likely to be different for each sample that is drawn from a population. It can, therefore, be thought of as a random variable, whose properties can be described with a probability distribution. The probability distribution of a sample statistic is known as a sampling distribution.
According to a key result in statistics known as the Central Limit Theorem, the sampling distribution of the sample mean is normal if one of two things is true:
The underlying population is normal
The sample size is at least 30
Two moments are needed to compute probabilities for the sample mean; the mean of the sampling distribution equals:
The standard deviation of the sampling distribution (also known as the standard error) can take on one of two possible values:
This is the appropriate choice for a "small" sample; for example, the sample size is less than or equal to 5 percent of the population size.
If the sample is "large," the standard error becomes:
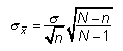
Probabilities may be computed for the sample mean directly from the standard normal table by applying the following formula: