Moments are summary measures of a probability distribution, and include the expected value, variance, and standard deviation. The moments of the geometric distribution depend on which of the following situations is being modeled:
The number of trials required before the first success takes place
The number of failures that occur before the first success
Just as with the binomial distribution, the geometric distribution has a series of simplified formulas for computing these moments.
How to calculate the expected value of the geometric distribution
The expected value of the geometric distribution when determining the number of trials required until the first success is
The expected value of the geometric distribution when determining the number of failures that occur before the first success is
For example, when flipping coins, if success is defined as "a heads turns up," the probability of a success equals p = 0.5; therefore, failure is defined as "a tails turns up" and 1 – p = 1 – 0.5 = 0.5. On average, there'll be (1 – p)/p = (1 – 0.5)/0.5 = 0.5/0.5 = 1 tails before the first heads turns up.
Notice how the two results provide the same information; it takes an average of two flips to get the first heads, or on average there should be one tails before the first heads turns up.
How to compute the variance and standard deviation of the geometric distribution
The variance and standard deviation of the geometric distribution when determining the number of trials required until the first success or when determining the number of failures that occur before the first success are
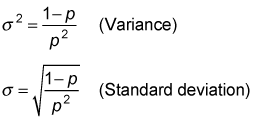
For example, suppose you flip a coin until the first heads turns up. The expected number of trials required until the first heads turns up is
The variance is






