The higher the frequency of an economic time series, the more likely it is to display seasonal patterns. For example, retail sales figures often exhibit a significant increase around the winter holidays. When you’re dealing with quarterly data, this increase is likely to be reflected with larger values in the fourth quarter of each year.
However, with monthly data, the change is more evident with even sharper increases in sales during the months of November and December.
The most common models capturing seasonal patterns include dummy variables representing the frequency with which the data were collected (usually quarter or month dummies).
A typical seasonal pattern is modeled with the specification
where S variables are your season dummy variables and the various alpha are the season coefficients representing the impact of each season, on average, on the dependent variable. If an alpha is positive, then the dependent variable increases during that season. If an alpha is negative, then the dependent variable decreases during that season.
The figure uses STATA to graph the log of monthly souvenir sales from 1987 to 1993 and estimate a seasonal pattern model. The dummy variables capturing the month of each observation have already been created.
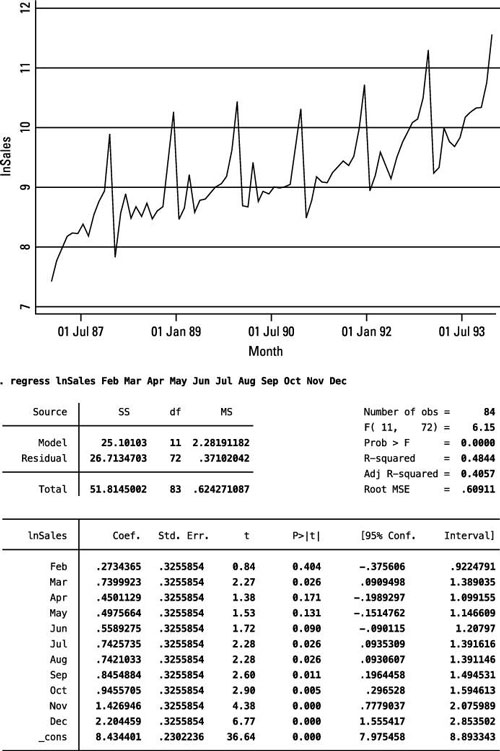
Given the depiction of the time series here, you can deduce that December will have significantly larger sales figures in comparison to other months. Using January as the reference month, several months have significantly larger sales figures. In comparison to January, sales are 74 percent larger in March and increase by more than 200 percent, on average, in December.





