If you use natural log values for your dependent variable (Y) and keep your independent variables (X) in their original scale, the econometric specification is called a log-linear model. These models are typically used when you think the variables may have an exponential growth relationship.
For example, if you put some cash in a saving account, you expect to see the effect of compounding interest with an exponential growth of your money! The original model in these types of scenarios isn’t linear in parameters, but a log transformation generates the desired linearity.
Consider the following model of value in a savings fund that depends on your initial investment, your return, and the length of time in which the funds are invested: Yt = Y0(1 + r)t, where Ytrepresents the value of the fund at time t, Y0 is the initial investment in the savings fund, and r is the growth rate.
Labor economists are also interested in similar functions because individuals usually have some initial earning power that can be supplemented with investments in skill acquisition. These human capital functions deal with the amount of money an individual can expect to earn depending on his or her initial abilities and investments in education, training, experience, and so on.
A generic exponential growth function can be written as Y = Y0(1 + r)X, where the value of Y for a given X can be derived only if the growth rate (r) is known. The growth rate can be estimated, but a log transformation must be used to estimate using OLS.
If you begin with an exponential growth model and take the log of both sides, you end up with ln Y = ln Y0 + Xln (1 + r), where ln Y0is the unknown constant and ln (1 + r) is the unknown growth rate plus 1 (in natural log form). You end up with the following model:
You can estimate this model with OLS by simply using natural log values for the dependent variable (Y) and the original scale for the independent variables (X). It’s known as a log-linear model.
After estimating a log-linear model, the coefficients can be used to determine the impact of your independent variables (X) on your dependent variable (Y). The coefficients in a log-linear model represent the estimated percent change in your dependent variable for a unit change in your independent variable. The coefficient
provides the instantaneous rate of growth.
Using calculus with a simple log-linear model, you can show how the coefficients should be interpreted. Begin with the model
and differentiate it to obtain
The term on the right-hand-side is the unit-change in X, and the term on the left-hand-side is the percent change in Y, so
provides the instantaneous rate of growth for Y associated with a unit change in X.
The compounded growth rate is considered to be a more accurate estimate of the impact of X. After estimating a log-linear model, you can calculate the compounded growth rate (r) as
Suppose you obtain the estimated regression
where Y is an individual’s wage and X is her years of education. The 0.08 value for
indicates that the instantaneous return for an additional year of education is 8 percent and the compounded return is 8.3 percent (e0.08 – 1 = 0.083).
If you estimate a log-linear regression, a couple outcomes for the coefficient on X produce the most likely relationships:
This log-linear function illustrates a positive impact from the independent variable, as shown in part (a).
This log-linear function depicts a negative impact from the independent variable, as shown in part (b).
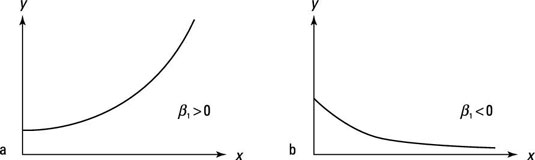
Regression coefficients in a log-linear model don’t represent the slope.





