Because samples are accessible, samples and confidence intervals are the primary data tool for understanding a business or processing Six Sigma performance situations. But samples can never give you an exact measure of what is going on in the underlying population. They’re inherently fuzzy! How sure can you be that your sample accurately enough reflects what is actually going on in the underlying population?
The key to objective decision-making lies in confidence intervals. They use the central limit theorem to quantify how much confidence you can place in any of your measurements or statistical conclusions from samples.
The measurement confidence we talk about here doesn’t address the capability of your system for acquiring measurements. Instead, measurement confidence assumes you have a perfect, ideal system for acquiring your measurements. This scenario should serve as another reminder of how important validating the capability of your measurement system is.
For example, say your factory has just produced 5,000 ballpoint pens. You want to know the average diameter of this population, so you randomly select 30 pens from the population, measure each of their diameters, and calculate the average to be 0.120 inches.
Suddenly, your boss rushes into your office and asks, “What’s the average diameter of our latest pens? Our customer just called and said it will reject the whole batch if the average is higher than 0.125 inches!” Your boss anxiously awaits your response. What do you say? How confident are you in your calculated average?
The central limit theorem says that if you repeat your 30-sample measurement, you’ll get a slightly different average. Your customer will, too, when checking its own sample. But how different will each calculation of the average be? Confidence intervals give you a way of quantifying how much variation will appear in repeated measurements and statistical calculations.
Knowing how to create confidence intervals, you’ll be able to tell your boss, “With 99.7 percent certainty, our average pen diameter will be within our customer’s requirement.”
You see averages every day. Unfortunately, very few of them are communicated with a confidence interval.
How to make decisions with large samples
When your sample size has more than 30 data points, you can calculate the confidence around the true population average (μ) as
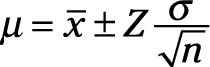
where
Z is the sigma value corresponding to the desired level of confidence you want to have.
σ is the calculated standard deviation from your sample.
n is the number of data points in your sample.


of the real population average. Further, 95 percent of calculated [neq16006]s are within
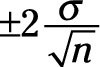
of the real population average. And 99.7 percent of calculated [neq16008]s are within
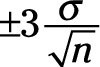
of the real population average. This formula works any time you have more than 30 measurements in your sample.
Make decisions with small samples
When you have only a few data points in your sample, you’re not able to get an accurate estimate of the population standard deviation σ. With these small samples, statisticians replace variable σ with s to communicate that you only have an inaccurate estimate of the population standard deviation from your sample.
So when your sample has anywhere from 2 to 30 data points, you have to use a different factor in place of Z. Statisticians call this new factor for small-sized samples t. t is more conservative because your smaller sample size lessens the accuracy of your calculated value for the standard deviation. For each desired confidence level, t is adjusted depending on how many data points are in your sample.
Using t, the formula for the confidence interval around the true population average becomes
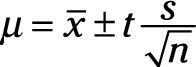
where the value for t depends on your desired level of confidence and the number of data points in your sample.





