Sometimes in a Six Sigma project, you will be faced with confidence intervals and proportions. When you calculate the number of successes out of a certain number of attempts — like “four out of five dentists recommend sugarless gum” — you can write this proportion (p) mathematically as
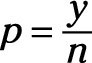
where y is the number of successes and n is the total number of attempts or trials.
Calculating a proportion creates yet another sampling distribution. The resulting confidence interval around a calculated proportion is
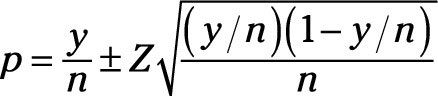
So, as an example, if you wanted to be 90-percent sure of the calculated proportion for the four out of five dentists, you would calculate the confidence interval as follows:
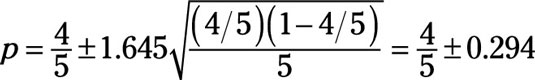
This result means that, with 90-percent confidence, the proportion of four out of five dentists really could be as small as one-half or as large as one.
In reality, proportions can never be less than zero or greater than one. So if your confidence interval for your proportion exceeds these natural limits, just adjust the confidence interval to the natural limit.
If you’re comparing the difference between two proportions, such as
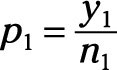
and
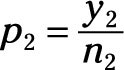
the confidence interval for this difference becomes
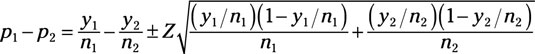
To illustrate this confidence interval, imagine you’re part of a company with two production lines. You suspect that your Toledo (T) plant produces a higher proportion of good items (yield) than your Buffalo (B) plant.
You select samples of size nT = nB = 300 from each plant and find that the number of good items from the Toledo plant (yT) is 213, while the number from the Buffalo plant (yB) is 189. That means that a 95-percent confidence interval for the difference between the Toledo and the Buffalo yields is
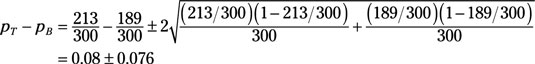
or, equivalently, [0.004, 0.156]. Because this confidence interval doesn’t include zero, you can conclude — with 95-percent confidence — that the Toledo plant produces, on average, a higher proportion of good items than the Buffalo plant.





