When you finish selecting, your set of selections is a combination of three of the nine good light bulbs together with a combination of three of the seven defective light bulbs. The probability of getting three good bulbs is a . . . well . . . combination of counting rules.
Each outcome of the selection of the good light bulbs can associate with all outcomes of the selection of the defective light bulbs, so the product rule is appropriate for the numerator. The denominator (the sample space) is the number of possible combinations of 6 items in a group of 16.
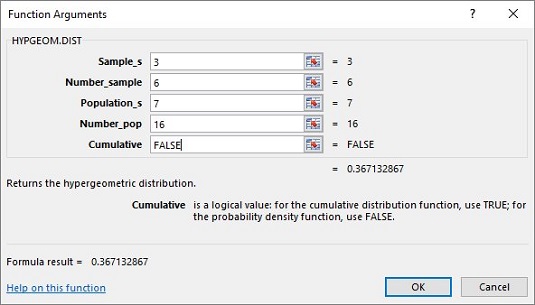
HYPGEOM.DIST calculates everything for you when you deal with the hypergeometric distribution. Here’s how to use it to work through the preceding example:
- Select a cell for
HYPGEOM.DIST’s answer. - From the Statistical Functions menu, select
HYPGEOM.DISTto open its Function Arguments dialog box. - In the Function Arguments dialog box, enter the appropriate values for the arguments.
In the Sample_s box, enter the number of successes in the sample. That number is 3 for this example.
In the Number_sample box, enter the number of items in the sample. The sample size for this example is 6.
In the Population_s box,enter the number of successes in the population. In this example that’s 7, the number of good light bulbs.
In the Number_pop box, enter the number of items in the population. The total number of light bulbs is 16, and that’s the population size.
In the Cumulative box, enter
FALSE. This gives the probability of the number of successes you entered in the Sample_s box. If you enterTRUE, the function returns the probability of, at most, that number of successes (for example, the cumulative probability). With values entered for all the arguments, the answer appears in the dialog box. The answer is 0.367 and some additional decimal places.Click OK to put the answer into the selected cell.
You can use HYP.GEOM.DIST to calculate pr(0) through pr(6) for this example. Then you use Excel’s graphics capabilities to graph the results. The objective is to help you visualize and understand the hypergeometric distribution.







