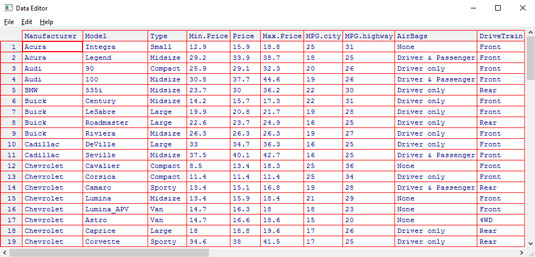
Cars93 data frame, which resides in the MASS package. This data frame holds data on 27 variables for 93 car models that were available in 1993.The figure shows part of the data frame in the Data Editor window that opens after you type
> edit(Cars93)
Graphing a distribution
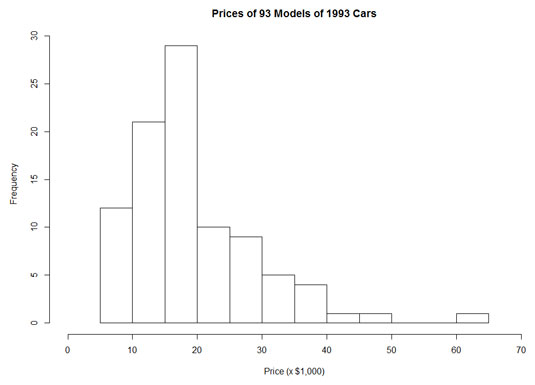
One pattern that might be of interest is the distribution of the prices of all the cars listed in theCars93 data frame. If you had to examine the entire data frame to determine this, it would be a tedious task. A graph, however, provides the information immediately. The following figure, a histogram, demonstrates.The histogram is appropriate when the variable on the x-axis is an interval variable or a ratio variable. With these types of variables, the numbers have meaning.
Here, Price is the independent variable, and Frequency is the dependent variable. In most (but not all) graphs, the independent variable is on the x-axis, and the dependent variable is on the y-axis.
Bar-hopping
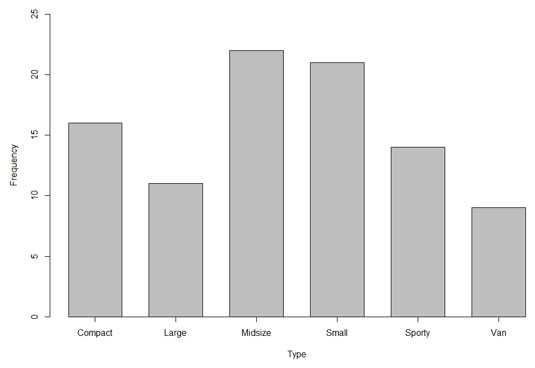
For nominal variables, numbers are just labels. In fact, the levels of a nominal variable (also called a factor) can be names. Case in point: Another possible point of interest is the frequencies of the different types of cars (sporty, midsize, van, and so on) in the data frame. So,"Type" is a nominal variable. If you looked at every entry in the data frame and created a table of these frequencies, it would look like the table.Types and Frequencies of Cars in the Cars93 data frame
| Type | Frequency |
| Compact | 16 |
| Large | 11 |
| Midsize | 22 |
| Small | 21 |
| Sporty | 14 |
| Van | 9 |
This figure shows this information in graphical form. This type of graph is a bar graph. The spaces between the bars emphasize that Type, on the x-axis, is a nominal variable.
Although the table is pretty straightforward, an audience would prefer to see the picture. Eyes that glaze over when looking at numbers often shine brighter when looking at pictures.
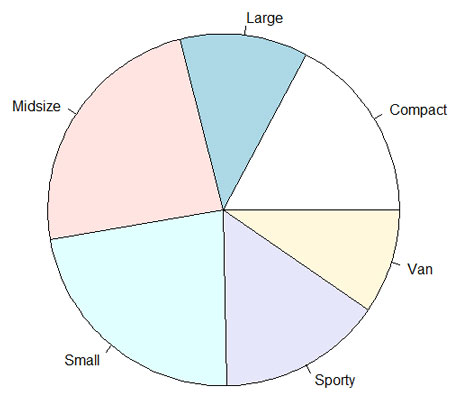
Slicing the pie
The pie graph is another type of picture that shows the same data in a slightly different way. Each frequency appears as a slice of a pie. In a pie graph, the area of the slice represents the frequency.The plot of scatter
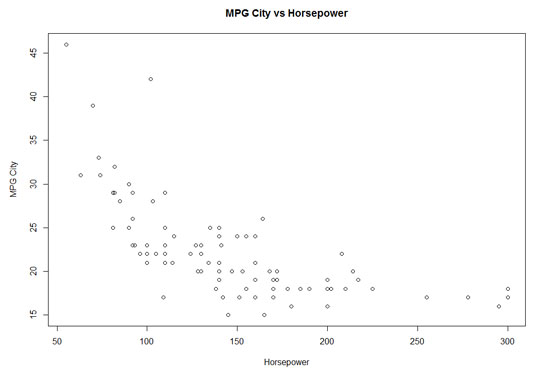
Another potential pattern of interest is the relationship between miles per gallon for city driving and horsepower. This type of graph is a scatter plot. This figure shows the scatter plot for these two variables.Each small circle represents one of the 93 cars. A circle's position along the x-axis (its x-coordinate) is its horsepower, and its position along the y-axis (its y-coordinate) is its MPG for city driving.
A quick look at the shape of the scatter plot suggests a relationship: As horsepower increases, MPG-city seems to decrease. (Statisticians would say "MPG-city decreases with horsepower.") Is it possible to use statistics to analyze this relationship and perhaps make predictions? Absolutely!
Of boxes and whiskers
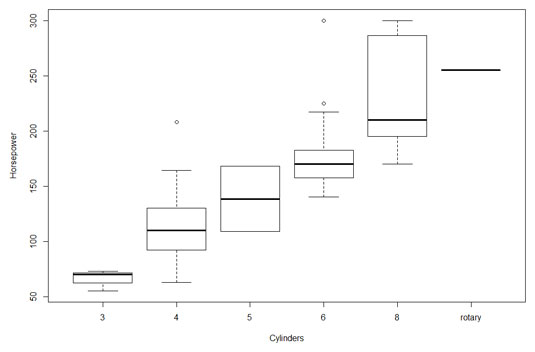
What about the relationship between horsepower and the number of cylinders in a car's engine? You would expect horsepower to increase with cylinders, and this figure shows that this is indeed the case. Invented by famed statistician John Tukey, this type of graph is called a box plot, and it's a nice, quick way to visualize data.Each box represents a group of numbers. The leftmost box, for example, represents the horsepower of cars with three cylinders. The black solid line inside the box is the median — the horsepower-value that falls between the lower half of the numbers and the upper half. The lower and upper edges of the box are called hinges. The lower hinge is the lower quartile, the number below which 25 percent of the numbers fall. The upper hinge is the upper quartile, the number that exceeds 75 percent of the numbers.
The elements sticking out of the hinges are called whiskers (so you sometimes see this type of graph referred to as a box-and-whiskers plot). The whiskers include data values outside the hinges. The upper whisker boundary is either the maximum value or the upper hinge plus 1.5 times the length of the box, whichever is smaller. The lower whisker boundary is either the minimum value or the lower hinge minus 1.5 times the length of the box, whichever is larger. Data points outside the whiskers are outliers. The box plot shows that the data for four cylinders and for six cylinders have outliers.
Note that the graph shows only a solid line for "rotary," an engine type that occurs just once in the data.