One of the most important decisions you make when specifying your econometric model is which variables to include as independent variables. Here, you find out what problems can occur if you include too few or too many independent variables in your model, and you see how this misspecification affects your results.
Omitting relevant variables
If a variable that belongs in the model is excluded from the estimated regression function, the model is misspecified and may cause bias in the estimated coefficients.
You have an omitted variable bias if an excluded variable has some effect (positive or negative) on your dependent variable and it’s correlated with at least one of your independent variables.
The mathematical nature of specification bias can be expressed using a simple model. Suppose the true population model is given by
where X1 and X2 are the two variables that affect Y. But due to ignorance or lack of data, instead you estimate this regression:
which omits X2 from the independent variables. The expected value of
in this situation is
But this equation violates the Gauss-Markov theorem because
The magnitude of the bias can be expressed as
where
if the effect of X2 on Y and
is the slope from this regression:
which captures the correlation (positive or negative) between the included and excluded variable(s).
| Impact of Omitted Variable on Dependent Variable | Correlation between Included and Omitted Variable: | |
|---|---|---|
| Positive | Negative | |
| Positive | Positive bias | Negative bias |
| Negative | Negative bias | Positive bias |
In practice, you’re likely to have some omitted variable bias because it’s impossible to control for everything that affects your dependent variable. However, you can increase your chances of minimizing omitted variable bias by avoiding simple regression models (with one independent variable) and including the variables that are likely to be the most important theoretically (and possibly, but not necessarily statistically) in explaining the dependent variable.
Including irrelevant variables
If a variable doesn’t belong in the model and is included in the estimated regression function, the model is overspecified. If you overspecify the regression model by including an irrelevant variable, the estimated coefficients remain unbiased. However, it has an undesirable effect of increasing the standard errors of your coefficients.
In a simple regression model (with one independent variable), the estimated standard error of the regression coefficient for X is
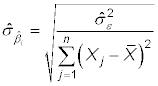
where
is the estimated variance of the error and
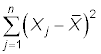
is the total variation in X.
If you include additional independent variables in the model, the estimated standard error for any given regression coefficient is given by
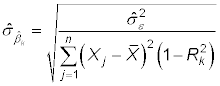
where
is the R-squared from the regression of Xk on the other independent variables or Xs. Because
the numerator decreases. An irrelevant variable doesn’t help explain any of the variation in Y, so without an offsetting decrease in
the standard error increases.
Just because your estimated coefficient isn’t statistically significant doesn’t make it irrelevant. A well-specified model usually includes some variables that are statistically significant and some that aren’t. Additionally, variables that aren’t statistically significant can contribute enough explained variation to have no detrimental impact on the standard errors.





