In quantum physics, when you are working in one dimension, the general particle harmonic oscillator looks like the figure shown here, where the particle is under the influence of a restoring force — in this example, illustrated as a spring.
The restoring force has the form Fx = –kxx in one dimension, where kx is the constant of proportionality between the force on the particle and the location of the particle. The potential energy of the particle as a function of location x is
This is also sometimes written as
Now take a look at the harmonic oscillator in three dimensions. In three dimensions, the potential looks like this:
Now that you have a form for the potential, you can start talking in terms of Schrödinger's equation:
Substituting in for the three-dimension potential, V(x, y, z), gives you this equation:
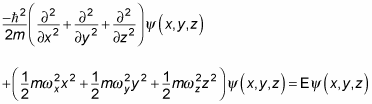
Take this dimension by dimension. Because you can separate the potential into three dimensions, you can write
Therefore, the Schrödinger equation looks like this for x:
Solving that equation, you get this next solution:
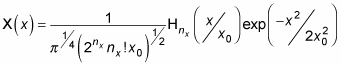
where
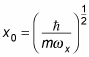
and nx = 0, 1, 2, and so on. The Hnx term indicates a hermite polynomial, which looks like this:
H0(x) = 1
H1(x) = 2x
H2(x) = 4x2 – 2
H3(x) = 8x3 – 12x
H4(x) = 16x4 – 48x2 + 12
H5(x) = 32x5 – 160x3 + 120x
Therefore, you can write the wave function like this:
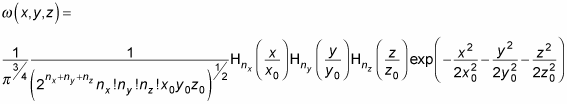
That's a relatively easy form for a wave function, and it's all made possible by the fact that you can separate the potential into three dimensions.
What about the energy of the harmonic oscillator? The energy of a one-dimensional harmonic oscillator is
And by analogy, the energy of a three-dimensional harmonic oscillator is given by
Note that if you have an isotropic harmonic oscillator, where
the energy looks like this:
As for the cubic potential, the energy of a 3D isotropic harmonic oscillator is degenerate. For example, E112 = E121 = E211. In fact, it's possible to have more than threefold degeneracy for a 3D isotropic harmonic oscillator — for example, E200 = E020 = E002 = E110 = E101 = E011.
In general, the degeneracy of a 3D isotropic harmonic oscillator is
where n = nx + ny + nz.





