When you have the eigenvalues of angular momentum states in quantum mechanics, you can solve the Hamiltonian and get the allowed energy levels of an object with angular momentum. The eigenvalues of the angular momentum are the possible values the angular momentum can take.
Here’s how to derive eigenstate equations with
Note that L2 – Lz2 = Lx2 + Ly2, which is a positive number, so
That means that
And substituting in
and using the fact that the eigenstates are normalized, gives you this:
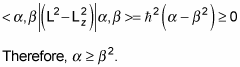
So there’s a maximum possible value of
which you can call
You can be clever now, because there has to be a state
such that you can’t raise
any more. Thus, if you apply the raising operator, you get zero:
Applying the lowering operator to this also gives you zero:
And because
that means the following is true:
Putting in
gives you this:
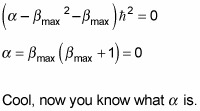
At this point, it’s usual to rename
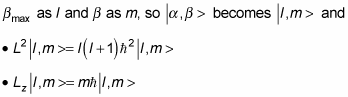
You can say even more. In addition to a
there must also be a
such that when you apply the lowering operator, L–, you get zero, because you can’t go any lower than
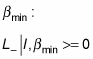
And you can apply L+ on this as well:
From
you know that
which gives you the following:
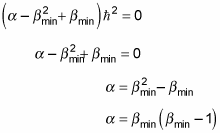
And comparing this equation to
gives you
Note that because you reach
by n successive applications of
you get the following:
Coupling these two equations gives you
Therefore,
can be either an integer or half an integer (depending on whether n is even or odd).
Because
and n is a positive number, you can find that
So now you have it:
The eigenstates are | l, m >.
The quantum number of the total angular momentum is l.
The quantum number of the angular momentum along the z axis is m.

For each l, there are 2l + 1 values of m. For example, if l = 2, then m can equal –2, –1, 0, 1, or 2.
You can see a representative L and Lz in the figure.
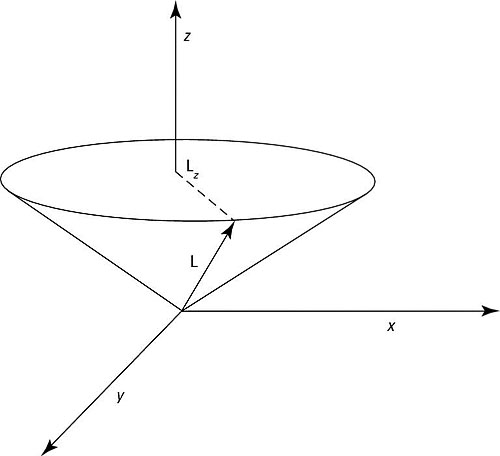
L is the total angular momentum and Lz is the projection of that total angular momentum on the z axis.





