How to Simplify and Split the Schrödinger Equation for Hydrogen

In quantum physics, you may need to simplify and split the Schrödinger equation for hydrogen. Here's the usual quantum mechanical Schrödinger equation for the hydrogen atom:

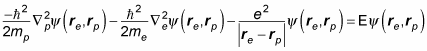
The problem is that you're taking into account the distance the proton is from the center of mass of the atom, so the math is messy. If you were to assume that the proton is stationary and that r_p = 0, this equation would break down to the following, which is much easier to solve:

Unfortunately, that equation isn't exact because it ignores the movement of the proton, so you see the more-complete version of the equation in quantum mechanics texts.

To simplify the usual Schrödinger equation, you switch to center-of-mass coordinates. The center of mass of the proton/electron system is at this location:

And the vector between the electron and proton is

r = r_e – r_p

Using vectors R and r instead of r_e and r_p makes the Schrödinger equation easier to solve. The Laplacian for R is

And the Laplacian for r is

How can you relate

to the usual equation's

After the algebra settles, you get

where M = m_e + m_p is the total mass and

is called the reduced mass. When you put together the equations for the center of mass, the vector between the proton and the electron, the total mass, and m, then the time-independent Schrödinger equation becomes the following:

Then, given the vectors, R and r, the potential is given by,

The Schrödinger equation then becomes

This looks easier — the main improvement being that you now have |r| in the denominator of the potential energy term rather than |r_e – r_p|.

Because the equation contains terms involving either R or r but not both, the form of this equation indicates that it's a separable differential equation. And that means you can look for a solution of the following form:

Substituting the preceding equation into the one before it gives you the following:

And dividing this equation by

gives you

Well, well, well. This equation has terms that depend on either

but not both. That means you can separate this equation into two equations, like this (where the total energy, E, equals E_R + E_r):

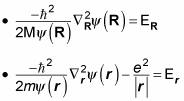
Multiplying

gives you

And multiplying

gives you

Now you have two Schrödinger equations, which you can solve independently.