How to Determine Harmonic Oscillator Eigenstates of a System

In quantum physics, when you have the eigenstates of a system, you can determine the allowable states of the system and the relative probability that the system will be in any of those states.

The commutator of operators A, B is [A, B] = AB – BA, so note that the commutator of

is the following:

This is equal to the following:

This equation breaks down to

And putting together this equation with the Hamiltonian,

Okay, with the commutator relations, you’re ready to go. The first question is: if the energy of state | n > is E_n, what is the energy of the state a | n >? Well, to find this, rearrange the commutator

Then use this to write the action of

like this:

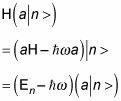
So a | n > is also an eigenstate of the harmonic oscillator, with energy

not E_n. That’s why a is called the annihilation or lowering operator: It lowers the energy level of a harmonic oscillator eigenstate by one level.

So what’s the energy level of

You can write that like this:

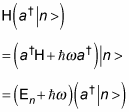
All this means that

is an eigenstate of the harmonic oscillator, with energy

not just E_n — that is, the

raises the energy level of an eigenstate of the harmonic oscillator by one level.

So now you know that

You can derive the following from these equations:

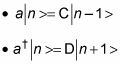
C and D are positive constants, but what do they equal? The states |n – 1> and |n + 1> have to be normalized, which means that n – 1|n – 1> = n + 1|n + 1> = 1. So take a look at the quantity using the C operator:

And because |n – 1> is normalized, n – 1|n – 1> = 1:

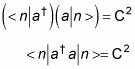
But you also know that

the energy level operator, so you get the following equation:

n | N | n > = C²

N | n > = n | n >, where n is the energy level, so

n n | n > = C²

However, n | n > = 1, so

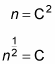
This finally tells you, from a | n > = C | n – 1 >, that

That’s cool — now you know how to use the lowering operator, a, on eigenstates of the harmonic oscillator.

What about the raising operator,

First you rearrange the commutator

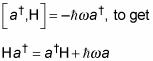
Then you follow the same course of reasoning you take with the a operator to show the following:

So at this point, you know what the energy eigenvalues are and how the raising and lowering operators affect the harmonic oscillator eigenstates.