Combine the Solutions for Small r and Large r in the Schrödinger Equation

When you apply the quantum mechanical Schrödinger equation for a hydrogen atom, you need to put together the solutions for small r and large r. The Schrödinger equation gives you a solution to the radial Schrödinger equation for a hydrogen atom as follows:

where f(r) is some as-yet-undetermined function of r. Your next task is to determine f(r), which you do by substituting this equation into the radial Schrödinger equation, giving you the following:

Performing the substitution gives you the following differential equation:

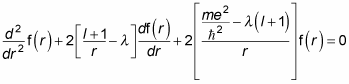
Quite a differential equation, eh? But just sit back and relax — you solve it with a power series, which is a common way of solving differential equations. Here’s the power-series form of f(r) to use:

Substituting the preceding equation into the one before it gives you

Changing the index of the second term from k to k – 1 gives you

Because each term in this series has to be zero, you have

Dividing by r^k–2 gives you

This equation gives the recurrence relation of the infinite series,

That is, if you have one coefficient, you can get the next one using this equation. What does that buy you? Well, take a look at the ratio of a_k/a_k–1:

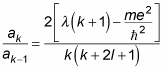
Here’s what this ratio approaches as k goes to infinity:

This resembles the expansion for e^x, which is

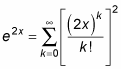
As for e^2x, the ratio of successive terms is

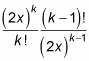
And in the limit

the ratio of successive expansion coefficients of e^2xapproaches 2/k:

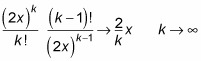
That’s the case for e^2x. For f(r), you have

Comparing these two equations, it’s apparent that

The radial wave function, R_nl(r), looks like this:

where

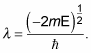
Plugging the form you have for f(r),

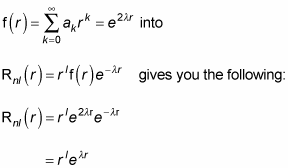
Okay, should you be overjoyed? Well, no. Here’s what the wave function

looks like:

And substituting in your form of R_nl(r) from this equation gives you