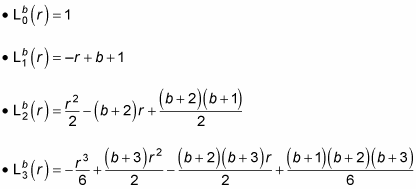Calculate the Wave Function of a Hydrogen Atom Using the Schrödinger Equation

If your quantum physics instructor asks you to find the wave function of a hydrogen atom, you can start with the radial Schrödinger equation, R_nl(r), which tells you that

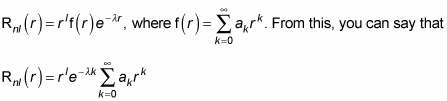
The preceding equation comes from solving the radial Schrödinger equation:

The solution is only good to a multiplicative constant, so you add such a constant, A_nl (which turns out to depend on the principal quantum number n and the angular momentum quantum number l), like this:

You find A_nl by normalizing R_nl(r).

Now try to solve for R_nl(r) by just flat-out doing the math. For example, try to find R₁₀(r). In this case, n = 1 and l = 0. Then, because N + l + 1 = n, you have N = n – l – 1. So N = 0 here. That makes R_nl(r) look like this:

And the summation in this equation is equal to

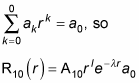
And because l = 0, r^l = 1, so

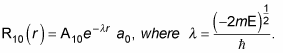
Therefore, you can also write

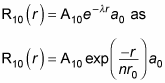
where r₀ is the Bohr radius. To find A₁₀ and a₀, you normalize

to 1, which means integrating

over all space and setting the result to 1.

and integrating the spherical harmonics, such as Y₀₀, over a complete sphere,

gives you 1. Therefore, you’re left with the radial part to normalize:

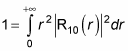
Plugging

into

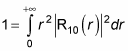
gives you

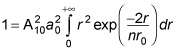
You can solve this kind of integral with the following relation:

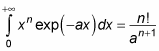
With this relation, the equation

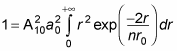
becomes

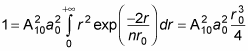
Therefore,

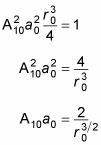
This is a fairly simple result. Because A₁₀ is just there to normalize the result, you can set A₁₀ to 1 (this wouldn’t be the case if

involved multiple terms). Therefore,

That’s fine, and it makes R₁₀(r), which is

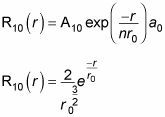
You know that

And so

becomes

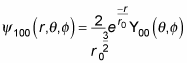
Whew. In general, here’s what the wave function

looks like for hydrogen:

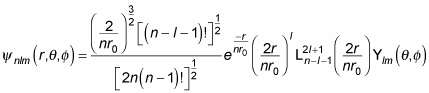
where

is a generalized Laguerre polynomial. Here are the first few generalized Laguerre polynomials: