Larger systems of linear equations involve more than two equations that go along with more than two variables. These larger systems can be written in the form Ax + By + Cz + . . . = K where all coefficients (and K) are constants. These linear systems can have many variables, and you can solve those systems as long as you have one unique equation per variable. In other words, while three variables need three equations to find a unique solution, four variables need four equations, and ten variables would have to have ten equations, and so on. You do not need to concern yourself with larger systems of non-linear equations. That would be far too complicated for pre-calc, and larger linear systems are complicated enough. For these types of systems, the solutions you can find vary widely:
You may find no solution.
You may find one unique solution.
You may come across infinitely many solutions.
The number of solutions you find depends on how the equations interact with one another. Because linear systems of three variables describe equations of planes, not lines (as two-variable equations do), the solution to the system depends on how the planes lie in three-dimensional space relative to one another. Unfortunately, just like in the systems of equations with two variables, you can’t tell how many solutions the system has without doing the problem. Treat each problem as if it has one solution, and if it doesn’t, you will either arrive at a statement that is never true (no solutions) or is always true (which means there are infinite solutions).
Typically, you must use the elimination method more than once to solve systems with more than two variables and two equations.
For example, suppose a problem asks you to solve the following system:
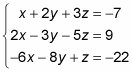
To find the solution(s), follow these steps:
Look at the coefficients of all the variables and decide which variable is easiest to eliminate.
With elimination, you want to find the least common multiple (LCM) for one of the variables, so go with the one that’s the easiest. In this case, you should eliminate the x variable.
Set apart two of the equations and eliminate one variable.
Looking at the first two equations, you have to multiply the top by –2 and add it to the second equation. Doing this, you get the following:

Set apart another two equations and eliminate the same variable.
The first and the third equations allow you to easily eliminate x again. Multiply the top equation by 6 and add it to the third equation to get the following:

Repeat the elimination process with your two new equations.
You should now have two equations with two variables:

You need to eliminate one of these variables. In this example, you eliminate the y variable by multiplying the top equation by 4 and the bottom by 7 and then adding the equations. Here’s what that gives you:

Solve the final equation for the variable that remains.
If 89z = –356, z = –4.
Substitute the value of the solved variable into one of the equations that has two variables to solve for another one.
In this example, you use the equation –7y – 11z = 23. Substituting, you have –7y – 11(–4) = 23, which simplifies to –7y + 44 = 23. Now finish the job:

Substitute the two values you now have into one of the original equations to solve for the last variable.
In this example, you use the first equation in the original system, which now becomes x + 2(3) + 3(–4) = –7. Simplify to get your final answer:

The solutions to this equation are x = –1, y = 3, and z = –4.
This process is called back-substitution because you literally solve for one variable and then work your way backwards to solve for the others. In this example, you went from the solution for one variable in one equation to two variables in two equations to the last step with three variables in three equations . . . always move from the more simple to the more complicated.





