How to solve inequalities
Inequalities are mathematical sentences that indicate that two expressions are something other than just equal. They’re expressed using the following symbols:Greater than: >
Greater than or equal to: ![]()
Less than: <
Less than or equal to: ![]()
Solving equations with inequalities is almost exactly the same as solving equations with equalities. There’s just one key exception: multiplying and dividing by negative numbers.
When you multiply or divide each side of an inequality by a negative number, you must switch the direction of the inequality symbol. In other words, < becomes > and vice versa.
This is also a good time to put together two key concepts: inequalities and absolute values, or absolute value inequalities. With these, you need to remember that absolute values have two possible solutions: one when the quantity in the absolute value bars is positive, and one when it’s negative. Therefore, you have to solve for these two possible solutions.The easiest way to solve for the two possible solutions in linear absolute value inequalities is to drop the absolute value bars and apply these rules:
 becomes
becomes  AND
AND  , which can also be written
, which can also be written 
 becomes
becomes  OR
OR 
The solutions for these absolute value inequalities can be expressed graphically, as you can see here. Note that the numbers representing the empty dots aren’t included in the solutions.
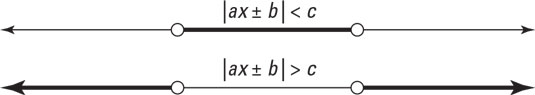 Graphical solutions for absolute value inequalities
Graphical solutions for absolute value inequalitiesWatch out for absolute value inequalities involving negative numbers. Here are two possible scenarios you may encounter:
- If the absolute value is less than or equal to a negative number, a solution doesn’t exist. Because an absolute value must be positive or zero, it can never be less than a negative number. For example,
 doesn’t have a solution.
doesn’t have a solution. - If the absolute value is greater than or equal to a negative number, there are infinitely many solutions, and the answer is “all real numbers.” An absolute value indicates a positive number or zero, which is always greater than a negative number. For instance, it doesn’t matter which number you plug into the equation |3x + 5| > –2, you always get a true statement. Therefore, the solution to this statement is “all real numbers.”
How to express inequality solutions in interval notation
You may or may not have experienced interval notation your earlier math studies. Interval notation, although strange sounding, is simply another way of expressing a solution set. Why have another way to write the same thing? Well, this notation is important to know because it’s the one most frequently used in pre-calculus and calculus.The key to writing a solution in interval notation is to locate the beginning and end of a set of solutions. You can do this by starting with inequality notation or by graphing the solution in order to visualize it.
After you locate your key points, you need to decide which of the following types of intervals you’re dealing with:- An open interval is always indicated by parentheses in interval notation. For instance, (1, 2) indicates 1 < x < 2. You show this open interval on a graph by using an open dot at the left endpoint, 1, and another open dot at the right endpoint, 2.
- A closed interval is always indicated by brackets in interval notation. For example, [0,3> means that
 . To graph this closed interval, use a filled dot at the left endpoint, 0, and another filled dot at the right endpoint, 3.
. To graph this closed interval, use a filled dot at the left endpoint, 0, and another filled dot at the right endpoint, 3. - A mixed interval is indicated by a mix of parentheses and brackets. For instance, both [–4, 3) and (4, 6> are the interval notation for a mixed interval. (Note that [–4,3) is the interval notation for the solution set
 , shown in the following figure.) You show a mixed interval on a graph by using either a filled dot at the left endpoint and an open dot at the right endpoint, or an open dot at the left endpoint and a filled dot at the right endpoint.
, shown in the following figure.) You show a mixed interval on a graph by using either a filled dot at the left endpoint and an open dot at the right endpoint, or an open dot at the left endpoint and a filled dot at the right endpoint.
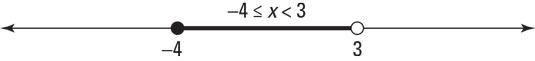 Graph of a mixed interval.
Graph of a mixed interval.To indicate a solution set that includes non-overlapping sections (also known as disjoint sets), you need to state all the intervals of the solution separated by the word or. For example, to write the solution set of
![]() or
or ![]() ,
,
you need to write both intervals in interval notation:

The symbol between the two sets is the union symbol, and it means that the solution can belong in one or the other interval.
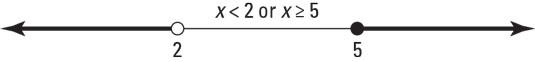 Graph of disjoint sets.
Graph of disjoint sets.You always use parentheses for infinity or negative infinity because they’re not real numbers.
Here are some more examples of dealing with interval notation.How to simply exponents and radicals
Radicals and exponents (also known as roots and powers) are fundamental algebra concepts. A radical signifies the principal root of a number and is indicated by the radical symbol. A square root of a number is a value that must be multiplied by itself to equal that number. For example, the square root of 9 is 3 because 3 multiplied by itself is 9. However (–3)(–3) is also equal to 9, but when asked to findWhen an exponent is a positive integer, it indicates the number of times a number (the base) is multiplied by itself. For example, 3 to the power of 4 is the same as 34 = 3 × 3 × 3 × 3 = 81.
When an exponent is a rational number, like in the expression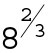 , the exponent isn’t equivalent to the number of times 8 is multiplied by itself. Fractional exponents have the root in the denominator and power in the numerator. To evaluate
, the exponent isn’t equivalent to the number of times 8 is multiplied by itself. Fractional exponents have the root in the denominator and power in the numerator. To evaluate 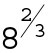 , you can write it as
, you can write it as or
or 
The denominator of a fractional exponent is the index of the radical. The index of the radical is the superscript you see before the radical sign. If the index of a radical is odd, then the value of the radical expression may be negative, but if the index of a radical is even, the result can’t be negative.
Roots and exponents are closely related to each other. In fact, they’re inverse operations. To solve an equation in which the variable is under a radical, simply raise both sides to the same power. For example, to solve ![]() , you need to square both sides to get x = 16. Similarly, you can often solve an equation in which the variable is raised to a power (or has an exponent) by taking the root of both sides. For instance, to solve x3 = 27, you can take the cube root of each side
, you need to square both sides to get x = 16. Similarly, you can often solve an equation in which the variable is raised to a power (or has an exponent) by taking the root of both sides. For instance, to solve x3 = 27, you can take the cube root of each side
![]()
to get x = 3. You can now use these facts to solve equations with radicals and exponents.
Sometimes it’s easier to solve expressions with radicals and exponents by rewriting them as rational exponents — exponents written as fractions. To do this, remember that the numerator of the rational exponent (the top number) is the power, and the denominator (the bottom number) is the index of the radical:
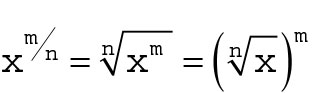
Rationalizing real numbers
It may sound irrational, but rationalizing can come in handy sometimes. To simplify fraction involving a radical expression, you often need to rationalize the denominator. In this section, you find a review and practice rationalizing the denominator.First up are monomials that need rationalizing. With monomials, you’re dealing with an expression and not an equation, so a big hint here is to remember equivalent fractions.
Keep in mind that a monomial is an expression, not an equation. You can’t simply square the term to find a solution because you can’t counterbalance that action. Instead, you need to multiply the numerator and denominator by the same term (which is the same as multiplying by 1). For example, if you need to rationalize the expression
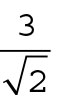 ,
,you can multiply the expression by  , which equals 1. You then get
, which equals 1. You then get
 .
.
The same idea works for other radicals with other indexes, but what you multiply by has to create a perfect power under the radical in the denominator.
To rationalize expressions with binomials in the denominator, you must multiply both the numerator and denominator by the conjugate of that denominator. A conjugate is a fancy name for the binomial that gives you the difference of two squares when multiplied by the first binomial. It’s found by changing the sign of the second term of the binomial.
For example, the conjugate of x + y is x – y because when you multiply the two conjugates (x + y)(x – y), you get x2 – y2, or the difference of two squares. So, to rationalize a denominator with a binomial, multiply the numerator and denominator by the conjugate and then simplify.
The steps look like this:






