Multiplying a sine or cosine function by a constant changes the graph of the parent function; specifically, you change the amplitude of the graph. When measuring the height of a graph, you measure the distance between the maximum crest and the minimum wave. Smack dab in the middle of that measurement is a horizontal line called the sinusoidal axis. Amplitude is the measure of the distance from the sinusoidal axis to the maximum or the minimum. The following figure illustrates this point further.
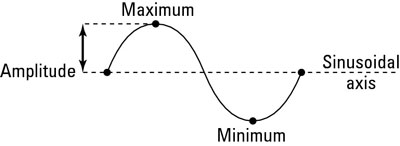
By multiplying a trigonometry function by certain values, you can make the graph taller or shorter:
Positive values of amplitudes greater than 1 make the height of the graph taller.

taller, and so on. For example,

you multiply the height of the original sine graph by 2 at every point. Every place on the graph, therefore, is twice as tall as the original.
If you remember that amplifying a sound makes it louder, you may have an easier time remembering that greater amplitudes increase the height.
Fraction values between 0 and 1 make the graph shorter.
You can say that

is even shorter. For example,

you multiply the parent graph's height by 1/5 at each point, making it that much shorter.
The change of amplitude affects the range of the function as well, because the maximum and minimum values of the graph change. Before you multiply a sine or cosine function by 2, for instance, its graph oscillated between –1 and 1; now it moves between –2 and 2.
Sometimes you multiply a trigonometric function by a negative number. That negative number doesn't make the amplitude negative, however! Amplitude is a measure of distance, and distance can't be negative. You can't walk –5 feet, for instance, no matter how hard you try. Even if you walk backward, you still walk 5 feet. Similarly,
its amplitude is still 5. The negative sign just flips the graph upside down.
The following table shows a comparison of an original input (x) and the value of
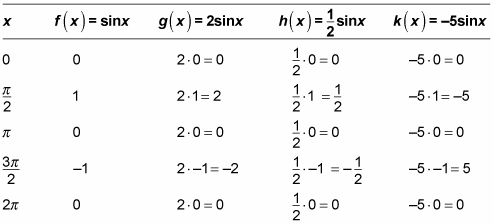
Don't worry; you won't have to re-create this table for any pre-calculus reasons. This is just to illustrate the comparison between the parent function and the more complicated functions. Keep in mind that this table displays only values of the sine function and transformations of it; you can easily do the same thing for cosine.
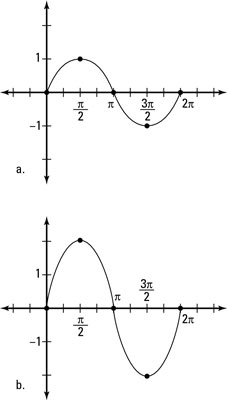
The figure just above illustrates what the graphs of sine look like after the transformations. Figure a is the graph of
Figure b is
The next figure shows some more examples of transformations of sine.
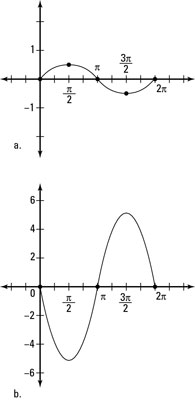
Figure a is
Figure b is





