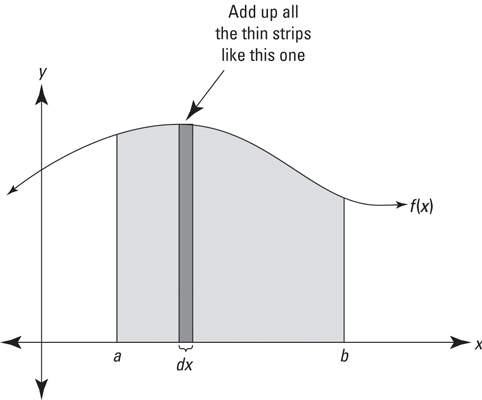
The most fundamental meaning of integration is to add up. And when you depict integration on a graph, you can see the adding up process as a summing up of thin rectangular strips of area to arrive at the total area under that curve, as shown in this figure.
You can calculate the shaded area in the above figure by using this integral:
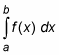
(Note that everything here involves definite integration as opposed to indefinite integration. Definite integration is where the elongated S integration symbol has limits of integration: the two little constants or numbers at the bottom and the top of the symbol. The elongated S without limits of integration indicates an indefinite integral or antiderivative.)
Look at the thin rectangle in the figure. It has a height of f(x) and a width of dx (a little bit of x), so its area (length times width, of course) is given by f(x) · dx. The above integral tells you to add up the areas of all the narrow rectangular strips between a and b under the curve f(x). As the strips get narrower and narrower, you get a better and better estimate of the area. The power of integration lies in the fact that it gives you the exact area by sort of adding up an infinite number of infinitely thin rectangles.
Regardless of what the tiny bits are that you’re adding up — they could be little bits of distance or volume or energy (or just area) — you can represent the summation as an adding up of the areas of thin rectangular strips under a curve. If the units on both the x and y axes are units of length, say, feet, then each thin rectangle measures so many feet by so many feet, and its area — length times width — is some number of square feet. In this case, the total area of all the rectangles between a and b gives you an area answer (though not necessarily the actual area under the curve because the scale may be different; for example, the actual shaded area in the above figure is a few square inches, but your answer could be a number of square miles if both axes were marked off in miles). The point is that in this case, you add up the areas of all the rectangles, and you get an area answer. Usually, however, even though you add up the areas of rectangles, your answer will not be an area answer.
Say the units on the x-axis are hours (t) and the y-axis is labeled in miles per hour, then, because rate times time equals distance, the area of each rectangle represents an amount of distance and the total area gives you the total distance traveled during the given time interval. Or if the x-axis is labeled in hours (t) and the y-axis in kilowatts of electrical power — in which case the curve, f(t), gives power usage as a function of time — then the area of each rectangular strip (kilowatts times hours) represents a number of kilowatt-hours of energy. In that case, the total area under the curve gives you the total number of kilowatt-hours of energy consumption between two points in time.

Another possibility is illustrated by the above lamp. Say you want to calculate the volume of the lamp’s base. The figure below shows how you would do this with integration. In the graph, the function A(x) gives the cross-sectional area of a thin pancake slice of the lamp as a function of its height measured from the bottom of the lamp. So this time, the h-axis is labeled in inches (that’s h as in height from the bottom of the lamp), and the y-axis is labeled in square inches, and thus each thin rectangle has a width measured in inches and a height measured in square inches. Its area, therefore, represents inches times square inches, or cubic inches of volume.
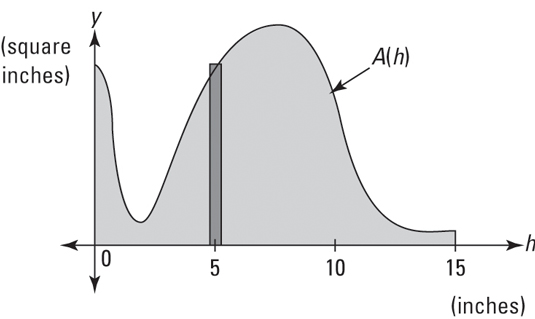
The area of the thin rectangle in this figure represents the volume of the thin pancake slice of the lamp 5 inches up from the bottom of the base. The total shaded area and thus the volume of the lamp’s base is given by the following integral:
Volume = (cross-sectional area) times (thickness)

This means that you add up the volumes of all the thin pancake slices from 0 to 15 inches (that is, from the bottom to the top of the lamp’s base), each slice having a volume given by A(h) (its cross-sectional area) times dh (its height or thickness).
To sum up — that’s a pun! — the mathematical expression to the right of any definite integration symbol always stands for a little bit of something, and integrating such an expression means to add up all the little pieces between some starting point and some ending point to determine the total between the two points.





