The following practice questions ask you to calculate shaded areas involving circles, squares, and triangles. Be careful, though: one of the questions may be a trap.
Practice questions
- A square is inscribed within a circle.
If it has a side length of
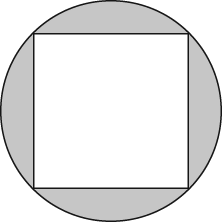 what is the area of the shaded portion of the drawing?
what is the area of the shaded portion of the drawing?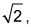
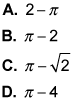
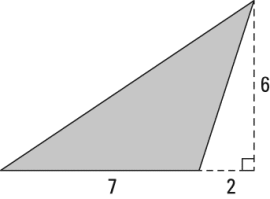
- What is the area of the shaded triangle?
A. 54 B. 42 C. 27 D. 21
Answers and explanations
- The correct answer is Choice (B).
First find the area of the square:
For the area of the circle, you need its radius. Cut the square in half, corner to corner, to form two 45-45-90 triangles, where each hypotenuse is the diameter of the circle. If the side of this triangle is
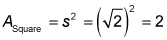 the hypotenuse is 2, because in a right triangle, the square of the hypotenuse is the sum of the squares of the other two sides:
the hypotenuse is 2, because in a right triangle, the square of the hypotenuse is the sum of the squares of the other two sides: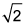 c2 = 4, so
c2 = 4, so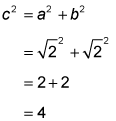 is the diameter of the circle, and the radius of the circle is half the diameter, or 1. Now for the area of the circle:
is the diameter of the circle, and the radius of the circle is half the diameter, or 1. Now for the area of the circle: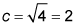 Subtract the area of the square from the area of the circle for your answer:
Subtract the area of the square from the area of the circle for your answer: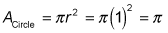
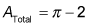
- The correct answer is Choice (D). For the area of a triangle, multiply the base by the height and divide by 2. The base of this triangle is 7, and the height is 6, for an area of 21. The 2 in the drawing has no bearing.

