All men and women are created equal, but not all expressions are. Remember that when you face the Praxis Core algebra exam. An inequality is a mathematical statement in which one side is (or may be) greater than or less than the other side. Some inequalities also suggest that the sides may be equal.
The signs used in inequalities are
<, which means “less than”
>, which means “greater than”
≤, which means “less than or equal to”
≥, which means “greater than or equal to”
The underlining of < and > to create ≤ and ≥means “or equal to.” Those signs indicate that the sides may be equal.
Here are some examples of inequalities and what they mean.
| 2x + 14 < 24 | “2x + 14 is less than 24.” |
| y + 6 > 11 | “y + 6 is greater than 11.” |
| 9w – 20 ≤ 34 | “9w – 20 is less than or equal to 34.” |
| 8b ≥48 | “8b is greater than or equal to 48.” |
An inequality sign always points to the side that is (or may be) the one that is less. You can also think of it as a mouth that’s trying to eat the greater side.
Like equations, inequalities can be solved when they involve only one variable of unknown value. For the most part, you solve inequalities the same way you do equations, but a couple of the rules change.
Following two more rules when solving inequalities
To solve an inequality, you use exactly the same rules you use to solve equations. However, unlike an equal sign, an inequality sign can change directions. Because of this, you must follow two extra rules when you solve inequalities. The sign in an inequality must change direction when either of the following happens:
Both sides are multiplied or divided by a negative number.
The sides are switched.
Consider the following:
3 < 7
You have a true inequality. However, what happens when you multiply both sides by a negative number?
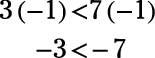
The resulting inequality is false; –3 is not less than –7. However, if the sign were to change direction, the resulting inequality would be true.
–3 > –7
The example illustrates that when both sides of an inequality are multiplied or divided by a negative number, the sign must change direction.
Now consider what happens when the two sides of an inequality are switched.
3 < 7
7 < 3
It’s true that 3 is less than 7, but 7 is not less than 3. Because the sides were switched, the direction of the sign has to change.
3 < 7
7 > 3
So 3 is less than 7, and 7 is greater than 3.
Here’s how you would solve this inequality: 47 ≥–10x – 3.
Isolate the term with the variable.
Add 3 to both sides to undo subtracting 3 from 10x.
47 + 3 ≥ –10x – 3 + 3
Combine like terms and simplify each side.
50 ≥ –10x.
Divide both sides of the equation by whatever number (coefficient) is in front of the x.
Divide both sides by –10 to undo multiplying x by –10.
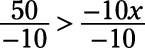
Simplify each side, and switch the direction of the sign because the sides were divided by a negative number.
–5 ≤ x
Switch the sides to make x the subject of the sentence, as a formality. Also change the direction of the sign because the sides were switched.
x ≥ –5
The solution to the inequality is x ≥ –5, which represents –5 and all numbers greater than –5. Any number that is –5 or greater will make the original inequality true.
Graphing inequalities
Inequalities with one variable can be graphed on the number line.
To graph an inequality on the number line, place a circle on the line at the point representing the solution. If the number used in the solution is included by the inequality, darken in the circle. This happens when ≤ or ≥ is used.
When < or > is used, the number used in the solution only marks the boundary of what makes the inequality true, and it’s not included in the set of numbers that make the inequality true. In those situations, make the circle hollow, not darkened. Next, darken in the part of the number line that includes the solution.
For example, if g ≥ 3, a ≥ sign is used, so g can be 3. Therefore, darken in the circle on the number line to show that 3 is included. Then, darken the part of the number line that includes everything greater than 3. If g < 4, g cannot be 4.
4 would only be the boundary for what g can be, so you would not darken in the circle on the number line.


