You will need to know geometric formulas for the Praxis Core Exam. Geometric figures have certain properties, and the number of dimensions they have is part of what decides what other properties they have. Line segments have a distance that can be referred to as length, width, or height.
Two-dimensional figures such as circles and triangles have area as well as parts with one-dimensional measurements. Three-dimensional geometric figures have the preceding properties plus volume. Formulas aren’t provided on the Praxis Core, so you’ll need to know the major area, surface area, and volume formulas.
Perimeter
The perimeter of a two-dimensional figure is the distance around it. To determine the perimeter of a polygon, you can add all the side measures. The following rectangle has a perimeter of 28 meters.
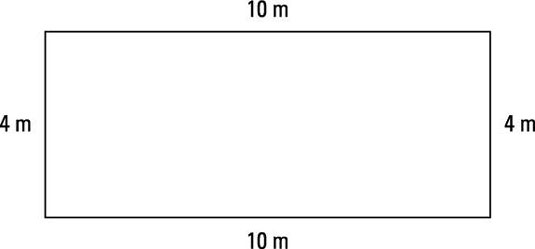
Because the opposite sides of a rectangle are congruent, a formula makes calculating the perimeter simpler than adding up all the side measures. Two of the sides have the length (l), and two sides have the width (w), so adding twice the length and twice the width gives the perimeter:
Perimeter of rectangle = 2l + 2w
Because the length and width of a square are the same, you can get the perimeter by multiplying the measure of one side by 4.
Circumference
The perimeter of a circle is the circle’s circumference. The formula for circumference involves π, which is the ratio of a circle’s circumference (C) divided by its diameter (d). Because all circles are similar, the ratio is the same for all circles.
π is an irrational number, so it never terminates or repeats in decimal form, but its value can be rounded to 3.14. Because circumference divided by diameter is π, circumference is diameter times π:

The diameter of a circle is twice the radius, so d = 2r. Therefore, C = π(2r). The formal way to write a term is with numbers before variables, and π is a number, so the official formula for the circumference is this:
C = 2πr
Remember that within a formula, any variable can represent an unknown in a problem. To find the value of the variable, fill every known number into the formula and solve for what is not yet known.
What is the radius of a circle with a circumference of 10π units?
(A) 10
(B) 5
(C) 100
(D) 5π
(E) 10π
The correct answer is Choice (B). You can use the formula for circumference and solve for r.
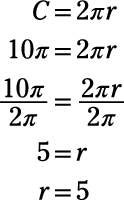
The other choices result from misuse of the circumference formula or using the wrong formula.
If getting the answer to a question involves the use of a formula with π in it, π may not appear as part of the answer choices. In that case, you need to use 3.14, the approximation for π, and do the calculation.
Area
A two-dimensional figure exists on a plane. The area of a two-dimensional figure is the amount of plane in it. In other words, area is a measure of how much room is inside a two-dimensional shape. Different shapes have different area formulas.
The area of a parallelogram is its base times its height. The base can be any side, but the height has to be the measure of a segment that is perpendicular to it and its opposite side.
area of parallelogram = bh
The area of the following parallelogram is its base times its height, or (7 cm)(10 cm), or 70 cm2.
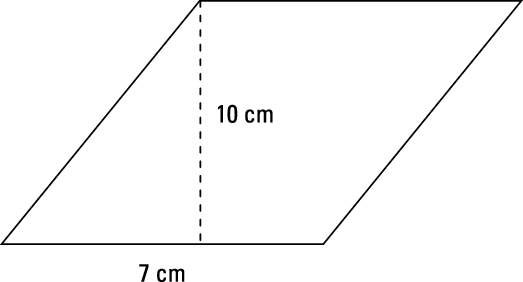
Any combination of base and height for a rectangle, which is a type of parallelogram, is a combination of length (l) and width (w), so the area of a rectangle is lw. All four sides of a square are congruent so all you have to do is multiply a side measure by itself.
If a parallelogram is cut at the vertices, the result is two congruent triangles. Also, any triangle can be put together with a congruent triangle to form a parallelogram. Because of this, every triangle has half the area of the parallelogram that can be formed by putting the triangle with an exact copy of itself. Therefore, the area of a triangle is not base times height, but half that:
The area of the following triangle is 1/2bh, or 1/2(8ft)(11ft), which is 44 ft2.
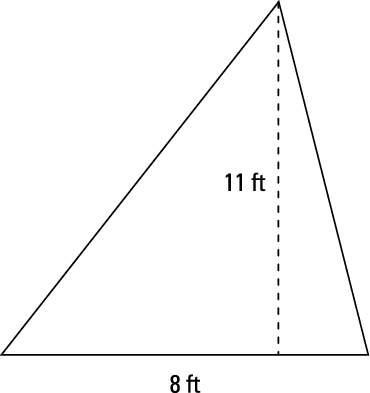
Make sure you know formulas for finding the areas of common shapes well because you’ll probably be asked at least one question about area on the Praxis.
| Figure | Area |
|---|---|
| Parallelogram | bh |
| Rectangle | lw |
| Square | s2 |
| Triangle | 1/2bh |
| Circle | ðr2 |
Finding the right volume
Volume is a three-dimensional measure. While surface area is the amount of plane on the surface of a three-dimensional figure, volume is the amount of space inside a three-dimensional figure. For rectangular solids and cylinders, the volume can be found by multiplying the base area by the height.
For rectangular solids, the volume is more specifically lwh since lw is the base area. The volume of a pyramid is 1/3 what the volume would be if the apex were a congruent base instead of a point, and a cone is 1/3 the volume of what it would be if the apex were a congruent base instead of a point.
That’s why the volume of a pyramid or cone is 1/3Bh instead of Bh. Remember that the bases of cones and cylinders are circles.
The height of one of these figures is the measure of a segment that goes from an apex or a base perpendicular to the plane on which the base, or other base, lies. If you have a question about these figures on the Praxis Core exam, the height will most likely be the measure of a segment that is perpendicular to the actual base. The dotted segments represent height.
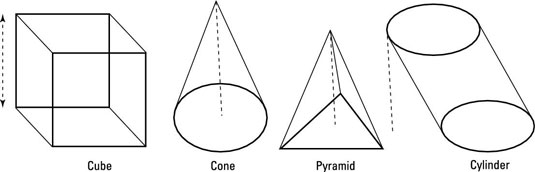
Check out the formulas for the volumes of major three-dimensional figures.
| Figure | Volume |
|---|---|
| Rectangular solid | Bh or lwh |
| Cylinder | ðr2h |
| Pyramid | 1/3Bh |
| Cone | 1/3ðr2h |
| Sphere | 4/3ðr3 |





