On the GED Mathematical Reasoning test, you may encounter systems of linear equations in the form of real-world word problems. When you encounter such a problem, you need to translate the words into math and formulate your equations as you normally do.
You'll end up with two equations, which is a great clue that you're dealing with a system of linear equations problem. The following practice questions ask you to calculate income based on gross sales for two levels of ticket prices, and the probability of winning a game based on multiple dice throws.
Practice questions
You and your friends have formed a rock band that is becoming increasingly popular. Your group headlined a recent concert and was promised 80% of the gross from the sales of adult tickets priced at $4.00 per person. Your group agreed not to receive any proceeds from the sales of student tickets priced at $1.50. The concert attendance was 220 people of all ages, and gross sales from tickets was $505.00. How much money was your band paid?
Bonny has invented a new game. It involves throwing two dice one after the other. If the difference between the numbers thrown is zero, the player wins. What are the chances of winning at Bonny's new game?
Answers and explanations
$224.00
To solve this problem, set up two equations, with S representing the number of students and A representing the number of adults. Gross sales from tickets was $505.00, which is the total received from adult tickets priced at $4.00 and student tickets priced at $1.50, so your first equation is this:
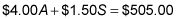
You also know that the total number of tickets sold is the number of adult tickets plus the number of student tickets, so your second equation is this:
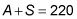
You can then use the substitution method. Solve for A in the second equation and you have A = 220 – S. Plug that in for A in the first equation and you have

If 150 student tickets were sold, then 220 – 150 = 70 adult tickets were sold at $4.00 each, bringing in $280. Your band received only 80 percent of that amount, or
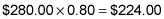
1 in 36
The chances of throwing any number with a die is 1 in 6 (a die has 6 faces). Having done so, the chances of throwing the same number with the same die is 1 in 6. In throwing the second die, the chances of any one number coming up is 1 in 6, but to win the player must get the same number as they got on the first throw. The chances of this are
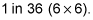
To express this as an equation, let C = the chance of a player winning in each turn be C, the chance of a player throwing a particular number be F, and the chance of the player throwing the same number on the second turn be S, then
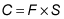
Therefore, C = 1 in 36.

