Familiarize yourself with inequalities for the ASVAB. All equations include one or more equal signs (=). However, some math problems look very much like equations, but they use signs other than the equal sign.
These problems are called inequalities. An equation states that each side of the equation separated by the equal sign is equal to the other. An inequality, on the other hand, says that the two sides separated by an inequality sign are not equal to each other.
Just as with equations, the solution to an inequality is all the values that make the inequality true. For the most part, you solve inequalities the same as you’d solve a normal equation. You need to keep some facts of inequality life need to keep in mind, however. Short and sweet, here they are:
Negative numbers are less than zero and less than positive numbers.
Zero is less than positive numbers but greater than negative numbers.
Positive numbers are greater than negative numbers and greater than zero.
Although there’s only one equal sign (=), several signs are associated with inequalities:
≠ means does not equal in the way that 3 does not equal 4, or 3 ≠ 4.
> means greater than in the way that 4 is greater than 3, or 4 > 3.
less than in the way the 3 is less than 4, or 3
≤ means less than or equal to in the way that x may be less than or equal to 4, or x ≤ 4.
≥ means greater than or equal to in the way that x may be greater than or equal to 3, or x ≥ 3.
You solve inequalities by using the same principles of algebra used to solve equations, with the exception of multiplying or dividing each side by a negative number. Take the following example:
Solve: 3x + 4
The inequality says that 3x plus 4 is less than 25. You solve it in the same way as you would the equation 3x + 4 = 25:
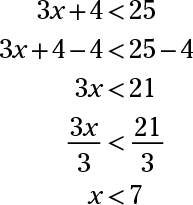
Although you solve inequalities the same way you solve equations, keep two important rules in mind when working with inequalities:
In algebra, if a = b, then b = a. In other words, you can swap the data on each side of the equal sign, and the equation means the same thing. So 2x + 4 = 18 and 18 = 2x + 4 are the same thing. This interchangeability doesn’t work with inequalities. So, 2x + 4 > 18 isn’t the same as 18 > 2x + 4.
When you swap the data in an inequality, you have to change the inequality sign to balance the inequality (keep the inequity true). So 2x + 4 > 18 is the same as 18 x + 4.
When you multiply or divide both sides of the inequality by a negative number, the inequality sign is reversed. So if you multiply both sides of the inequality 3 –16.





