Many of the problems you see on the ASVAB math subtests require you to perform calculation involving exponents and scientific notation. If that sounds confusing, don’t worry; it’s really not. Read on.
Advice about exponents
Exponents are an easy way to show that a number is to be multiplied by itself a certain number of times. For example, 52 is the same as 5 × 5, and 43 is the same as 4 × 4 × 4.
The number or variable that is to be multiplied by itself is called the base, and the number or variable showing how many times it’s to be multiplied by itself is called the exponent.
Here are important rules when working with exponents:
Any base raised to the power of one equals itself. For example, 61 = 6.
Any base raised to the zero power (except 0) equals 1. For example, 30 = 1.
In case you were wondering, according to most calculus textbooks, 00 is an “indeterminate form.” What mathematicians mean by “indeterminate form” is that in some cases it has one value, and in other cases it has another. This stuff is advanced calculus, however, and you don’t have to worry about it on the ASVAB math subtests.
To multiply terms with the same base, you add the exponents. For example, 72 × 73 = 75.
To divide terms with the same base, you subtract the exponents. For example, 45 ÷ 43 = 42.
If a base has a negative exponent, it’s equal to its reciprocal with a positive exponent. For example,
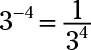
When a product has an exponent, each factor is raised to that power. For example, (5 × 3)3 = 53 × 33.
Scientific notation
Scientific notation is a compact format for writing very large or very small numbers. Although it’s most often used in scientific fields, you may find a question or two on the Mathematics Knowledge subtest of the ASVAB asking you to convert a number to scientific notation, or vice versa.
Scientific notation separates a number into two parts: a characteristic, always greater than or equal to 1 and less than 10, and a power of ten. Thus, 1.25 × 104 means 1.25 times 10 to the fourth power, or 12,500; 5.79 × 10–8 means 5.79 times 10 to the negative eighth power.
A negative exponent is equal to its reciprocal with a positive exponent, so 10–8 means 1/100,000,000. In this case, the scientific notation comes out to 0.0000000579.





