A word problem (also called a story problem or a problem in a setting) gives you information in words rather than in just equations and numbers. To answer an ACT word problem, you have to translate the provided information into one or more equations and then solve.
You can solve some word problems fairly easily. Jotting down the numbers in the problem can be useful to help get you focused and moving in the right direction. The following example word problems show you how.
Example 1
Seminar X brought in $700 in revenue and had 20 participants, each of whom paid the same amount. Seminar Y brought in $750 and had 15 participants, each of whom paid the same amount. How much more did each person pay for Seminar Y than Seminar X?
(A) $5
(B) $10
(C) $15
(D) $20
(E) The two seminars cost the same amount.
If you’re not immediately sure how to proceed, jot down the numbers in an orderly fashion:
This step only takes a moment and gets your brain moving. When you organize the information in this way, you may see that the next step involves division:
Now you can easily see that Seminar Y cost $15 more than Seminar X, so the correct answer is Choice (C).
Example 2
Jessica is in charge of stocking shelves at a supermarket. Today, she has already stocked 8 boxes that each contained 40 cans of soup, 12 boxes that each contained 24 cans of corned beef hash, and 4 boxes that each contained 60 cans of tuna. How many cans has Jessica stocked today?
(F) 148
(G) 310
(H) 624
(J) 848
(K) 1,020
Record the numbers in this question as follows:

Now multiply these numbers across (with or without your calculator, as needed) to get the number of cans in each set of boxes:
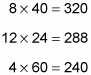
Finish by adding the results: 320 + 288 + 240 = 848. Therefore, the correct answer is Choice (J).
Some word problems are much easier to solve when you draw a sketch to organize your thoughts. This technique is especially helpful if you’re a visual learner. So if you like to draw, paint, or play video games, lead with your strength and try to find a visual way to express math problems whenever possible. The following example shows how to use a sketch to your advantage.
Example 3
The 12:00 p.m. eastbound train left the station at a constant speed of 40 miles per hour. At 12:45 p.m., the next eastbound train left the station at a constant speed of 60 miles per hour. Assuming neither train stops along the way, how far apart will the two trains be at 2:00 p.m.?
(A) 5 miles
(B) 10 miles
(C) 12 miles
(D) 15 miles
(E) 18 miles
This problem is difficult to visualize, so sketching out the information can help you arrive at the correct answer:
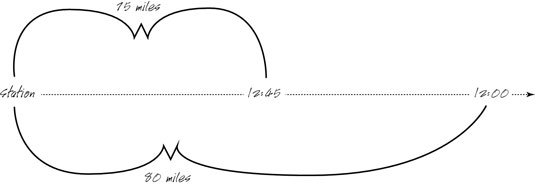
This figure helps illustrate a way into the problem: By 2:00 p.m., the 12:00 p.m. train has traveled for 2 hours at 40 miles per hour, so it’s 80 miles from the station. And the 12:45 p.m. train has traveled for 1 hour and 15 minutes at 60 miles per hour. The 1 hour accounts for 60 miles. The 15 minutes is a quarter of an hour, so this accounts for 15 miles. Thus, the 12:45 p.m. train is 75 miles from the station. As a result, the trains are 5 miles apart, making the correct answer Choice (A).





