Some math questions on the ACT will involve ratios and proportions. Both ratio and proportion problems involve comparing quantities, and they require that you know how to work with fractions and how to solve by using algebra.
A ratio is a comparison of two quantities based on the operation of division. For example, if a school has one teacher for every eight students, you can express the teacher-to-student ratio in any of the following ways:
Notice that this ratio expresses the ratio of teachers to students. Thus, the 1 goes before the 8 and, in the fraction, the 1 goes on top of the 8.
When answering an ACT question that includes a ratio, a good strategy is to express the ratio as an equivalent fraction. Then you can pull out all the tools you already have for working with fractions — for example, reducing, converting to decimals, and so forth.
Example 1
A company has a total of 150 employees, 25 of whom are managers. What is the ratio of managers to non-managers?
(A) 1 to 3
(B) 1 to 4
(C) 1 to 5
(D) 1 to 6
(E) 2 to 5
The company has 25 managers, so the remaining 125 employees are non-managers. Express this ratio as a fraction and then reduce it:
The ratio of managers to non-managers is 1 to 5, so the correct answer is Choice (C).
One of the most practical applications of the ratio is a proportion, which is an equation based on a ratio. For example, if you know the ratio of boys to girls, you can express this as a fraction, set it equal to another fraction that includes a variable, and then solve. The following example illustrates how this concept works.
Example 2
A summer camp has a boy-to-girl ratio of 8:11. If the camp has 88 boys, what is the total number of children at the camp?
(F) 121
(G) 128
(H) 152
(J) 176
(K) 209
Begin by setting up the proportion as the following equation:
Before continuing, notice that the ratio specifically mentions boys first and girls second, so this order is maintained in the equation. The camp has 88 boys, so substitute this number for Boys in the equation. You don’t know how many girls there are, so use the variable g. Here’s what your equation now looks like:
To find out how many girls are at the camp, solve for g using algebra. First, cross-multiply to get rid of the two fractions:
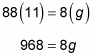
Now divide both sides by 8:
121 = g
The camp includes 121 girls and 88 boys, so you know it has a total of 209 children; therefore, the correct answer is Choice (K).





