Quantum physicists use large particle accelerators to discover more about particle scattering on the subatomic level. You can think of a scattering experiment in terms of particles in and particles out. The following figure shows an example where particles are being sent in a stream from the left and interacting with a target; most of them continue on unscattered, but some particles interact with the target and scatter.
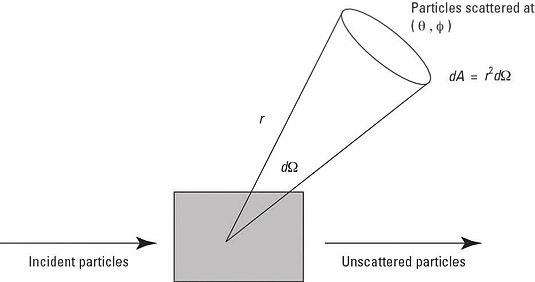
Those particles that do scatter do so at a particular angle in three dimensions — that is, you give the scattering angle as a solid angle,
The number of particles scattered into a specific
is proportional to a very important quantity in scattering theory: the differential cross section.
The differential cross section is given by
and it's a measure of the number of particles per second scattered into
per incoming flux. The incident flux, J (also called the current density), is the number of incident particles per unit area per unit time. So

The differential cross section
has the dimensions of area, so calling it a cross section is appropriate. The cross section is sort of like the size of the bull's eye when you're aiming to scatter incident particles through a specific solid angle.
The differential cross section is the cross section for scattering to a specific solid angle. The total cross section,
is the cross section for scattering of any kind, through any angle. So if the differential cross section for scattering to a particular solid angle is like the bull's eye, the total cross section corresponds to the whole target.
You can relate the total cross section to the differential cross section by integrating the following:





