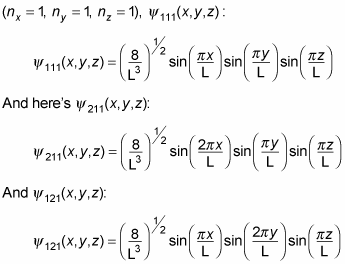In quantum physics, when working with a box potential, you can make things simpler by assuming that the box is actually a cube. In other words, L = Lx = Ly = Lz. When the box is a cube, the equation for the energy becomes

So, for example, the energy of the ground state, where nx = ny = nz = 1, is given by the following, where E111 is the ground state:
Note that there's some degeneracy in the energies; for example, note that
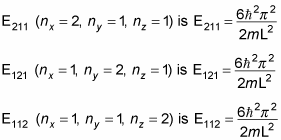
So E211 = E121 = E112, which means that the first excited state is threefold degenerate, matching the threefold equivalence in dimensions.
In general, when you have symmetry built into the physical layout (as you do when L = Lx = Ly = Lz), you have degeneracy.
The wave function for a cubic potential is also easier to manage than the wave function for a general box potential (where the sides aren't of the same length). Here's the wave function for a cubic potential:
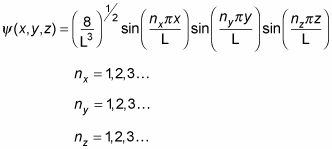
So, for example, here's the wave function for the ground state