In quantum physics, if you know the boundary conditions of a square well, you can find theenergy levels of an electron.
The equation
tells you that you have to use the boundary conditions to find the constants A and B. What are the boundary conditions? The wave function must disappear at the boundaries of an infinite square well, so
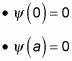
The fact that
tells you right away that B must be zero because cos(0) = 1. And the fact that
tells you that
Because sine is zero when its argument is a multiple of
this means that
Note that although n = 0 is technically a solution, it yields
for all x, which is not normalizable, so it’s not a physical solution — the physical solutions begin with n = 1.
This equation can also be written as
And because
you have the following equation, where n = 1, 2, 3, ... — those are the allowed energy states. These are quantized states, corresponding to the quantum numbers 1, 2, 3, and so on:
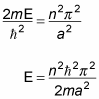
Note that the first physical state corresponds to n = 1, which gives you this next equation:
This is the lowest physical state that the particles can occupy. Just for kicks, put some numbers into this, assuming that you have an electron, mass
confined to an infinite square well of width of the order of the Bohr radius (the average radius of an electron’s orbit in a hydrogen atom); let’s say
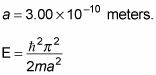
gives you this energy for the ground state:
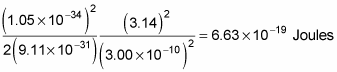
That’s a very small amount, about 4 electron volts (eV — the amount of energy one electron gains falling through 1 volt). Even so, it’s already on the order of the energy of the ground state of an electron in the ground state of a hydrogen atom (13.6 eV), so you can say you’re certainly in the right quantum physics ballpark now.

