In quantum physics, you can solve for the allowable energy states of a particle, whether it is bound, or trapped, in a potential well or is unbound, having the energy to escape.
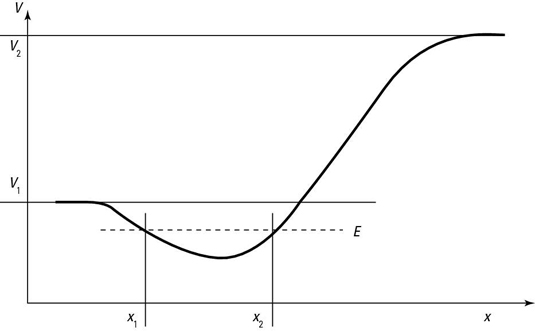
Take a look at the potential in the following figure. The dip, or well, in the potential, means that particles can be trapped in it if they don’t have too much energy.
The particle’s kinetic energy summed with its potential energy is a constant, equal to its total energy:
If its total energy is less than V1, the particle will be trapped in the potential well, as you see in the figure; to get out of the well, the particle’s kinetic energy would have to become negative to satisfy the equation, which is impossible according to classical mechanics.
Quantum-mechanically speaking, there are two possible states that a particle with energy E can take in the potential given by the figure — bound and unbound.
Bound states happen when the particle isn’t free to travel to infinity — it’s as simple as that. In other words, the particle is confined to the potential well.
A particle traveling in the potential well you see in the figure is bound if its energy, E, is less than both V1 and V2. In that case, the particle moves between x1 and x2. It is possible to discover the particle outside this region.
A particle trapped in such a well is represented by a wave function, and you can solve the Schrödinger equation for the allowed wave functions and the allowed energy states. You need to use two boundary conditions (the Schrödinger equation is a second-order differential equation) to solve the problem completely.
Bound states are discrete — that is, they form an energy spectrum of discrete energy levels. The Schrödinger equation gives you those states. In addition, in one-dimensional problems, the energy levels of a bound state are not degenerate — that is, no two energy levels are the same in the entire energy spectrum.
If a particle’s energy, E, is greater than the potential (V1 in the figure), the particle can escape from the potential well. There are two possible cases: V12 and E > V2.
Case 1: Particles with energy between the two potentials (V12)
If V12, the particle in the potential well has enough energy to overcome the barrier on the left but not on the right. The particle is thus free to move to negative infinity, so its classically allowed x region is between
Here, the allowed energy values are continuous, not discrete, because the particle isn’t completely bound. The energy eigenvalues are not degenerate — that is, no two energy eigenvalues are the same.
The Schrödinger equation,
is a second-order differential equation, so it has two linearly independent solutions; however, in this case, only one of those solutions is physical and doesn’t diverge.
The wave equation in this case turns out to oscillate for x x2 and to decay rapidly for x > x2.
Case 2: Particles with energy greater than the higher potential (E > V2)
If E > V2, the particle isn’t bound at all and is free to travel from negative infinity to positive infinity.
The energy spectrum is continuous and the wave function turns out to be a sum of a wave moving to the right and one moving to the left. The energy levels of the allowed spectrum are therefore doubly degenerate.





