In quantum physics, you can find commutators of angular momentum, L. First examine Lx, Ly, and Lz by taking a look at how they commute; if they commute (for example, if [Lx, Ly] = 0), then you can measure any two of them (Lx and Ly, for example) exactly. If not, then they’re subject to the uncertainty relation, and you can’t measure them simultaneously exactly.
Okay, so what’s the commutator of Lx and Ly? Using Lx = YPz – ZPy and Ly = ZPx – XPz, you can write the following:
[Lx, Ly] = [YPz – ZPy, ZPx – XPz]
You can write this equation as
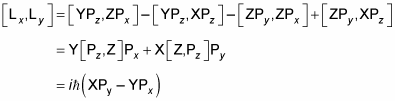
But
So Lx and Ly don’t commute, which means that you can’t measure them both simultaneously with complete precision. You can also show that
Because none of the components of angular momentum commute with each other, you can’t measure any two simultaneously with complete precision. Rats.
That also means that the Lx, Ly, and Lz operators can’t share the same eigenstates. So what can you do? How can you find an operator that shares eigenstates with the various components of L so that you can write the eigenstates as | l, m >?
The usual trick here is that the square of the angular momentum, L2, is a scalar, not a vector, so it’ll commute with the Lx, Ly, and Lz operators, no problem:
[L2, Lx] = 0
[L2, Ly] = 0
[L2, Lz] = 0
Okay, cool, you’re making progress. Because Lx, Ly, and Lz don’t commute, you can’t create an eigenstate that lists quantum numbers for any two of them. But because L2 commutes with them, you can construct eigenstates that have eigenvalues for L2 and any one of Lx, Ly, and Lz. By convention, the direction that’s usually chosen is Lz.

