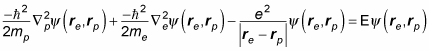Using the Schrödinger equation tells you just about all you need to know about the hydrogen atom, and it's all based on a single assumption: that the wave function must go to zero as r goes to infinity, which is what makes solving the Schrödinger equation possible.
Hydrogen atoms are composed of a single proton, around which revolves a single electron. You can see how that looks in the following figure.
Note that the proton isn't at the exact center of the atom — the center of mass is at the exact center. In fact, the proton is at a radius of rp from the exact center, and the electron is at a radius of re.
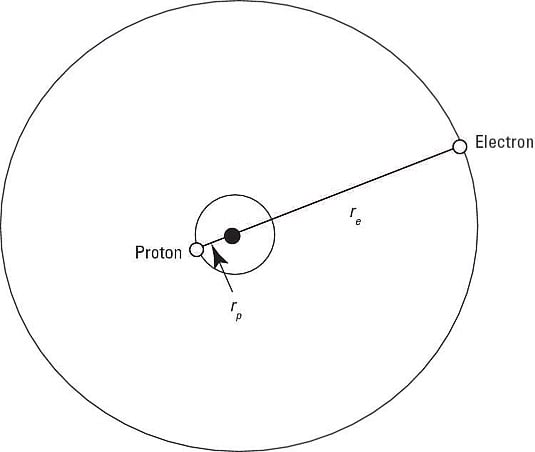
So what does the Schrödinger equation, which will give you the wave equations you need, look like? Well, it includes terms for the kinetic and potential energy of the proton and the electron. Here's the term for the proton's kinetic energy:
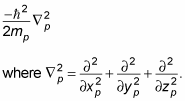
Here, xp is the proton's x position, yp is the proton's y position, and zp is its z position.
The Schrödinger equation also includes a term for the electron's kinetic energy:
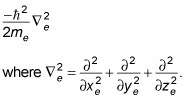
Here, xe is the electron's x position, ye is the electron's y position, and ze is its z position.
Besides the kinetic energy, you have to include the potential energy, V(r), in the Schrödinger equation, which makes the time-independent Schrödinger equation look like this:
where
is the electron and proton's wave function.
The electrostatic potential energy, V(r), for a central potential is given by the following formula, where r is the radius vector separating the two charges:
As is common in quantum mechanics, you use the CGS (centimeter-gram-second) system of units, where
So the potential due to the electron and proton charges in the hydrogen atom is
Note that r = re – rp, so the preceding equation becomes
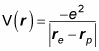
which gives you this Schrödinger equation: