Determining the Energy Levels of a Particle in a Box Potential

In quantum physics, to be able to determine the energy levels of a particle in a box potential, you need an exact value for X(x) — not just one of the terms of the constants A and B. You have to use the boundary conditions to find A and B. What are the boundary conditions? The wave function must disappear at the boundaries of the box, so

• X(0) = 0

• X(L_x) = 0

So the fact that

tells you right away that B must be 0, because cos(0) = 1. And the fact that X(L_x) = 0 tells you that X(L_x) = A sin(k_xL_x) = 0. Because the sine is 0 when its argument is a multiple of

this means that

And because

it means that

That's the energy in the x component of the wave function, corresponding to the quantum numbers 1, 2, 3, and so on. The total energy of a particle of mass m inside the box potential is E = E_x + E_y + E_z. Following

you have this for E_y and E_z:

So the total energy of the particle is E = E_x + E_y + E_z, which equals this:

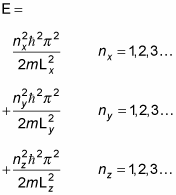
And there you have the total energy of a particle in the box potential.