Create Symmetric and Antisymmetric Wave Functions for a Two-Particle System

If your quantum physics instructor asks you to create symmetric and antisymmetric wave functions for a two-particle system, you can start with the single-particle wave functions:

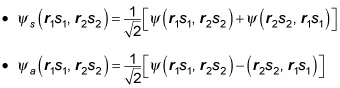
By analogy, here’s the symmetric wave function, made up of two single-particle wave functions:

And here’s the antisymmetric wave function, made up of the two single-particle wave functions:

where n_i stands for all the quantum numbers of the ith particle.

Note in particular that

when n₁ = n₂; in other words, the antisymmetric wave function vanishes when the two particles have the same set of quantum numbers — that is, when they’re in the same quantum state. That idea has important physical ramifications.

You can also write

like this, where P is the permutation operator, which takes the permutation of its argument:

And also note that you can write

like this:

where the term (–1)^P is 1 for even permutations (where you exchange both r₁s₁ and r₂s₂ and also n₁ and n₂) and –1 for odd permutations (where you exchange r₁s₁ and r₂s₂ but not n₁ and n₂; or you exchange n₁ and n₂ but not r₁s₁ and r₂s₂).

In fact, people sometimes write

in determinant form like this:

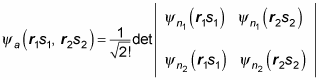
Note that this determinant is zero if n₁ = n₂.