A less extreme form of the old saying "garbage in equals garbage out" is "fuzzy in equals fuzzy out." Random fluctuations in one or more measured variables produce random fluctuations in anything you calculate from those variables. This process is called the propagation of errors. You need to know how measurement errors propagate through a calculation that you perform on a measured quantity.
Here's a simple way to estimate the SE of a variable (Y) that's calculated from almost any mathematical expression that involves a single variable (X). Starting with the observed X value (Xo), and its standard error (SE), just do the following 3-step calculation:
Evaluate the expression, substituting the value of Xo – SE for X in the formula. Call the result Y1.
Evaluate the expression, substituting the value of Xo + SE for X in the formula. Call the result Y2.
The SE of Y is simply (Y2 – Y1)/2.
Here's an example that shows how (and why) this process works.
Suppose you measure the diameter (d) of a coin as 2.3 centimeters, using a caliper or ruler that you know (from past experience) has an SE of ± 0.2 centimeters. Now say that you want to calculate the area (A) of the coin from the measured diameter.
If you know that the area of a circle is given by the formula
you can immediately calculate the area of the coin as
which you can work out on your calculator to get 4.15475628 square centimeters. Of course, you'd never report the area to that many digits because you didn't measure the diameter very precisely. So just how precise is your calculated area? In other words, how does that ± 0.2-centimeter SE of d propagate through the formula to give the SE of A?
One way to answer this question would be to consider a margin of error (ME) around the observed diameter (d) that goes from one SE below d to one SE above d. The ME is always two SEs wide. In the coin example, the diameter's ME extends from 2.3 – 0.2 to 2.3 + 0.2, or from 2.1 to 2.5 centimeters.
Now figure out the areas corresponding to the diameters at the lower and upper ends of the ME. Using 2.1 for d in the area formula gives A = 3.46, and using 2.5 for d gives A = 4.91. So the ME for the area of the coin goes from 3.46 to 4.91 square centimeters.
The width of this ME is 4.91 – 3.46, or 1.45 square centimeters, which represents two SEs for the area. So the SE of the area is 1.45/2, or 0.725 square centimeter.
The curved line represents the formula A = π/4) x d2. The dark arrows show how the measured diameter (2.3 centimeters), when plugged into the formula, produces a calculated area of about 4.15 square centimeters. The lighter colored gray arrows represent the lower and upper ends of the ME and show how the ME for the diameter produces an ME for the area.
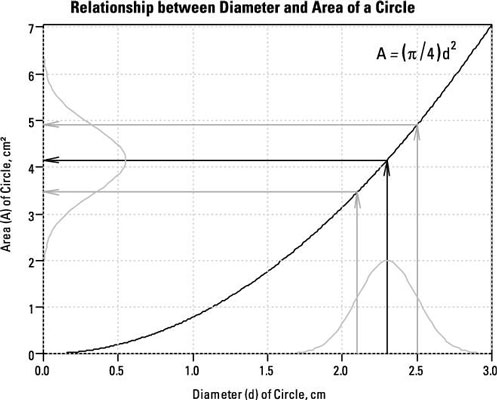
The SE of the area depends on the SE of the diameter and the slope of the curve. In fact, the SE of the area is equal to the SE of the diameter multiplied by the slope of the curve.
Unfortunately, the simple procedure illustrated in this example can't be generalized to handle functions of two or more variables, such as calculating a person's body mass index from height and weight.
Mathematicians have derived a very general formula for calculating (approximately) how SEs in one or more variables propagate through any expression involving those variables, but it's very complicated, and to use it you have to be really good at calculus or you'll almost certainly make mistakes along the way.
Fortunately, there are much better alternatives:
You can use some simple error-propagation formulas for simple expressions.
Even easier, you can go to a web page that does the error-propagation calculations for functions of one or two variables.
You can use a very general simulation approach that can easily analyze how errors propagate through even the most complicated expressions, involving any number of variables.





