When you're using right triangles to define trig functions, the trig function sine, abbreviated sin, has input values that are angle measures and output values that you obtain from the ratio opposite/hypotenuse. The figure shows two different acute angles, and each has a different value for the function sine.
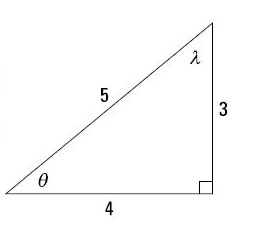
The two values are
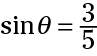
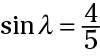
The sine is always the measure of the opposite side divided by the measure of the hypotenuse. Because the hypotenuse is always the longest side, the number on the bottom of the ratio will always be larger than that on the top.
For this reason, the output of the sine function will always be a proper fraction — it'll never be a number equal to or greater than 1 unless the opposite side is equal in length to the hypotenuse (which only happens when your triangle is a single segment or you're working with circles).
Even if you don't know both lengths required for the sine function, you can calculate the sine if you know any two of the three lengths of a triangle's sides. For example, to find the sine of angle alpha in a right triangle whose hypotenuse is 10 inches long and adjacent side is 8 inches long:
Find the length of the side opposite alpha.
Use the Pythagorean theorem, a2 + b2 = c2, letting a be 8 and c be 10. When you input the numbers and solve for b, you get

So, the opposite side is 6 inches long.
Use the ratio for sine, opposite over hypotenuse.





