The graphs of the trig functions have many similarities and many differences. The graphs of the sine and cosine look very much alike, as do the tangent and cotangent, and then the secant and cosecant have similarities. But those three groupings do look different from one another.
The one characteristic that ties them all together is the fact that they're periodic, meaning they repeat the same curve or pattern over and over again, in either direction along the x-axis.
The graph of y = sin x.
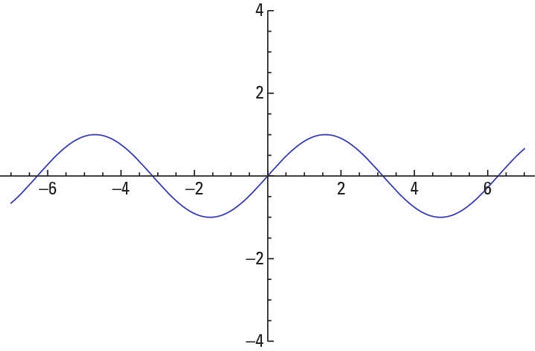
The graph of the sine function is a nice, continuous wave that rolls along gently and keeps repeating itself. The domain, or x-values, of the sine function includes all angles in degrees or all real numbers in radians, so the curve has no breaks or holes.
The graph of y = cos x.
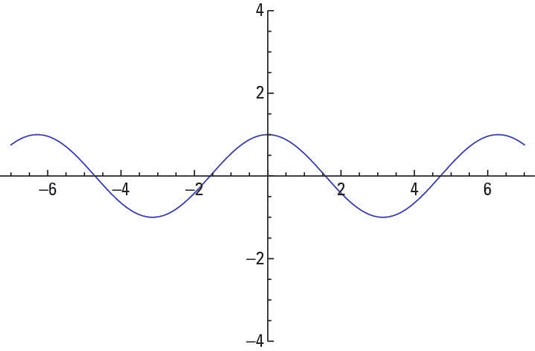
The relationship between the sine and cosine graphs is that the cosine is the same as the sine shifted to the left by 90 degrees.
The graph of y = tan x.
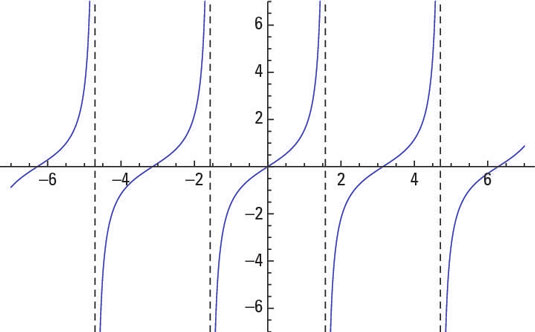
The tangent function can be written as the ratio of the sine divided by the cosine.
The graph of y = cot x.
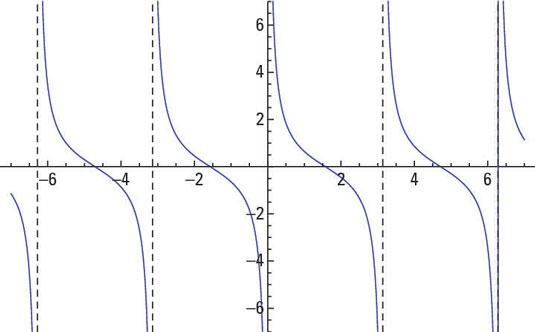
The graphs of the tangent function lay the groundwork for the graphs of the cotangent. After all, they’re cofunctions and reciprocals, and have all sorts of connections.
The graph of y = sec x.
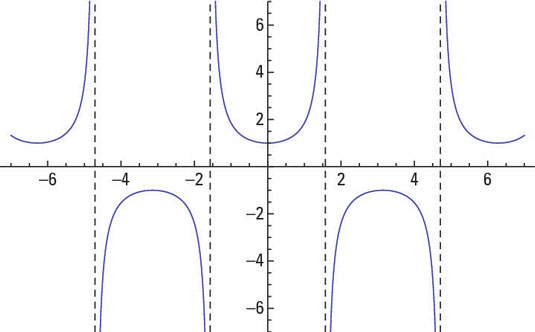
The techniques that you use to graph the secant curve parallel those that you use to graph the cosecant. First, identify the asymptotes by determining where the reciprocal of secant — cosine — is equal to 0. Then sketch in that reciprocal, and you can determine the turning points and general shape of the secant graph.
The graph of y = csc x.
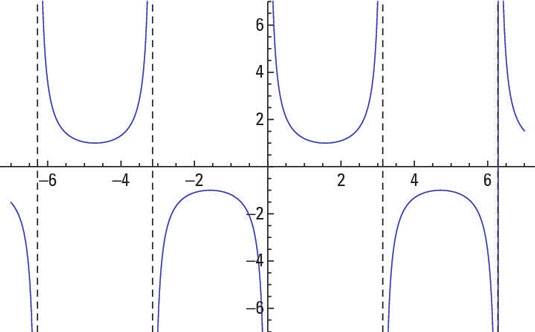
The cosecant function is the reciprocal of the sine function (meaning, the cosecant equals 1 divided by the sine).




