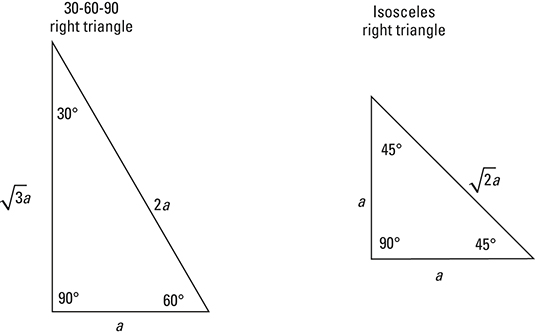
Every right triangle has the property that the sum of the squares of the two legs is equal to the square of the hypotenuse (the longest side). The Pythagorean theorem is written: a2 + b2 = c2. What’s so special about the two right triangles shown here is that you have an even more special relationship between the measures of the sides — one that goes beyond (but still works with) the Pythagorean theorem. When you have a 30-60-90 right triangle, the measure of the hypotenuse is always twice the measure of the shortest side, and the other leg is always
or about 1.7 times as big as the shortest side. With the isosceles right triangle, the two legs measure the same, and the hypotenuse is always
or about 1.4 times as long as those two legs.