Anytime you're trying to estimate a number from a population (like the average gas price in the United States), you include a margin of error. You need to accurately calculate the sample size needed to get a particular margin of error you want.
For the three practice questions here, consider that:
A sociologist is interested in the average age women get married. The sociologist knows that the population standard deviation of age at first marriage is three years for women and hasn't changed for the last 60 years. The sociologist would like to demonstrate with 95% confidence that the mean age of the first marriage for women.
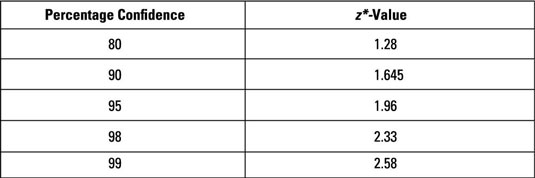
The following table provides the z*- values for selected (percentage) confidence levels.
Sample questions
If the sociologist can sample only 50 women, what will the margin of error be?
Answer: plus/minus 0.83 years
The formula for margin of error when estimating a population mean is

where z* is the value from the table for a given confidence level (95% in this case, or 1.96),

is the standard deviation (3 years), and n is the sample size (50).
Now, substitute the numbers into the formula and solve:

With 50 women in the sample, the sociologist has a margin of error of plus/minus 0.83 years.
If the sociologist can sample 100 women, what will the margin of error be?
Answer: plus/minus 0.59 years
The formula for margin of error when estimating a population mean is

where z* is the value from the table for a given confidence level (95% in this case, or 1.96),

is the standard deviation (3 years), and n is the sample size (100).
Now, substitute the numbers into the formula and solve:

With this sample size, the margin of error is plus/minus 0.59 years.
What is the smallest number of participants the sociologist can sample to estimate the average nuptial age for the population, with a margin of error of only two years?
Answer: 9
To solve this problem, you have to do a little algebra, using the general formula for margin of error when estimating a population mean:

Here, z* is the value from the table for a given confidence level (95% in this case, or 1.96),

is the population standard deviation (3 years), and n is the sample size.
To find the sample size, n, you have to rearrange the formula for margin of error: Multiply both sides by the square root of n, divide both sides by the margin of error, and square both sides (note that a sample size can only be positive). Here are the steps:

Now to solve the problem at hand, substitute the values into the formula:

You can't have a fraction of a participant and you need to make sure the margin of error is less than or equal to two years, so round up to 9 participants.
Note: Even if the result was a number that you'd normally round down (like 8.123), you still always round up to the next greatest integer when solving for sample size.
If you need more practice on this and other topics from your statistics course, visit 1,001 Statistics Practice Problems For Dummies to purchase online access to 1,001 statistics practice problems! We can help you track your performance, see where you need to study, and create customized problem sets to master your stats skills.





