You need to become more familiar with the possibilities for rewriting trigonometric expressions. A trig identity is really an equivalent expression or form of a function that you can use in place of the original. The equivalent format may make factoring easier, solving an application possible, and (later) performing an operation in calculus more manageable.
The trigonometric identities are divided into many different classifications. These groupings help you remember the identities and make determining which identity to use in a particular substitution easier.
In a classic trig identity problem, you try to make one side of the equation match the other side. The best way to do so is to work on just one side — the left or the right — but sometimes you need to work on both sides to see just how to work the problem to the end.
In pre-calculus, you’ll work with the basic trigonometric identities in the following ways:
Determining which trig functions are reciprocals of one another
Creating Pythagorean identities from a right triangle whose hypotenuse measures 1 unit
Determining the sign of identities whose angle measure is negated
Matching up trig functions and their co-functions
Using the periods of functions in identities
Making the most of selected substitutions into identities
Working on only one side of the identity
Figuring out where to go with an identity by working both sides at once
Don’t let common mistakes trip you up; keep in mind that when working on trigonometric identities, some challenges will include the following:
Keeping track of where the 1 goes in the Pythagorean identities
Remembering the middle term when squaring binomials involving trig functions
Correctly rewriting Pythagorean identities when solving for a squared term
Recognizing the exponent notation
Practice problems
Prove the trig identity. Indicate your first identity substitution:

Answer: use the reciprocal identity
Because each term contains a function and its reciprocal, using reciprocal identities will simplify the terms quickly.
First, replace

with its reciprocal identity,

and

with its reciprocal identity:

Then simplify the complex fractions.

Finally, replace

with 1, using the Pythagorean identity: 1 = 1
Determine the missing term or factor in the identity by changing all functions to those using sine or cosine:

Answer: 1
Use the reciprocal identity to replace csc2x and use the ratio identity to replace tan2x:
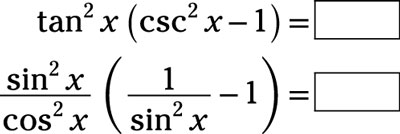
Distribute

simplify, and then combine the two terms:

Rewrite the Pythagorean identity, sin2x + cos2x = 1, by subtracting sin2x from each side to get cos2x = 1 – sin2x. Replace the numerator of the fraction in the identity with cos2x:

The missing term is 1.





