Co-function identities may pop up in trig proofs. If you see the expression pi/2 – x in parentheses inside any trig function, you need to use a co-function identity for the proof. Follow the steps to prove this equality:
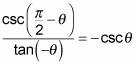
Replace any trig functions with pi/2 in them with the appropriate co-function identity.

Simplify the new expression.
You have many trig identities at your disposal, and you may use any of them at any given time. Now is the perfect time to use an even/odd identity for tangent:

Then use the reciprocal identity for secant and the sines and cosines definition for tangent to get

Finally, rewrite this complex fraction as the multiplication of two simpler fractions, the top fraction multiplied by the reciprocal of the bottom fraction:

Cancel anything that's both in the numerator and the denominator and then simplify. This step gives you

Now, bring back the right side of the equality, and rewrite the last line of the proof as






